
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=10^2+8^2\)
=> \(BC^2=164\)
=> \(BC=12,8\left(cm\right)\)
b, Xét Δ ABE và Δ HBE, có :
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác \(\widehat{ABC}\))
\(\widehat{BAE}=\widehat{BHE}=90^o\)
BE là cạnh chung
=> Δ ABE = Δ HBE (g.c.g)
=> AB = HB
Xét Δ ABH, có : AB = HB (cmt)
=> Δ ABH cân tại B
c,
Gọi O là giao điểm của tia AH và BE
Xét Δ cân ABH, có :
BO là tia phân giác \(\widehat{ABH}\)
=> BO là đường cao
=> \(BO\perp AH\)
=> \(BE\perp AH\)

Bài 6:
a: Đặt 4x-1/2=0
=>4x=1/2
hay x=1/8
b: Đặt (x-1)(x+1)=0
=>x-1=0 hoặc x+1=0
=>x=1 hoặc x=-1


Ta có:A=\(\left[\frac{1}{2}+\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^4+....+\left(\frac{1}{2}\right)^{99}\right]\)
\(\frac{1}{2}A\)=\(\frac{1}{2}\)\(\left[\frac{1}{2}+\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+\left(\frac{1}{4}\right)^4+....+\left(\frac{1}{2}\right)^{99}\right]\)
\(\frac{1}{2}A\)=\(\left[\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^4+\left(\frac{1}{2}\right)^5+...+\left(\frac{1}{2}\right)^{100}\right]\)
\(\frac{1}{2}A-A\)=\(\left[\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^4+\left(\frac{1}{2}\right)^5+...+\left(\frac{1}{2}\right)^{100}\right]\)-\(\left[\frac{1}{2}+\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^4+....+\left(\frac{1}{2}\right)^{99}\right]\)
\(-\frac{1}{2}A\)=\(\left(\frac{1}{2}^{100}\right)-\frac{1}{2}\)
\(-\frac{1}{2}A\)=\(-\frac{1}{2}\)
A=\(-\frac{1}{2}:\left(-\frac{1}{2}\right)\)
A=1
Chúc bạn học tốt!
 Mng giúp mình bài 1, 2, 3, 4 nha(vẽ hình luôn). Cảm ơn nhiều 🤩
Mng giúp mình bài 1, 2, 3, 4 nha(vẽ hình luôn). Cảm ơn nhiều 🤩

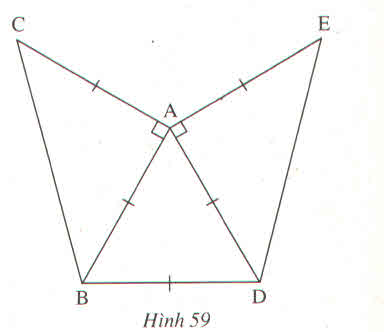
 các bạn giúp mình làm bài này nha, cảm ơn nhiều
các bạn giúp mình làm bài này nha, cảm ơn nhiều 




where hình
tự vẽ chứ nhỉ ?!!!