TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 5 2017
2006 . 125 + \(\dfrac{1000}{126}\) . 2005 - 888 = 265774,6984
MN
1
Q
27 tháng 3 2017
Tính:
\(B=\dfrac{3}{13.19}+\dfrac{3}{19.25}+...+\dfrac{3}{613.619}\)
\(B=\dfrac{1}{2}.\left(\dfrac{6}{13.19}+\dfrac{6}{19.25}+...+\dfrac{6}{613.619}\right)\)
\(B=\dfrac{1}{2}.\left(\dfrac{6}{13}-\dfrac{6}{19}+\dfrac{6}{19}-\dfrac{6}{25}+...+\dfrac{6}{613}-\dfrac{6}{619}\right)\)
\(B=\dfrac{1}{2}.\left(\dfrac{6}{13}-\dfrac{6}{619}\right)\)
\(B=\dfrac{1}{2}.\dfrac{3636}{8047}=\dfrac{1818}{8047}\)
31 tháng 1 2017
a, S= 1-2+3-4+...........+99-100
=(1-2)+(3-4)+.............+(99-100)
= (-1)+(-1)+...........+(-1)
=-50
b, B = 1+3-5-7+9+11-.........-397-399
= (1+3-5-7)+(9+11-13-15)+........+(393+395-397-399)
= (-8)+(-8)+...........+(-8)
= -400
NN
2
NT
0
DT
Đỗ Thanh Hải
CTVVIP
3 tháng 3 2017
Đây bạn
Viết lại bài toán cần chứng minh
13+23+33+..n3=(1+2+3+...+n)213+23+33+..n3=(1+2+3+...+n)2
Với n=1;n=2n=1;n=2 thì đẳng thức hiển nhiên đúng, hay chính là câu a,b đó 
Giả sử đẳng thức đúng với n=kn=k
Tức 13+23+33+...k3=(1+2+3+4..+k)213+23+33+...k3=(1+2+3+4..+k)2
Ta sẽ chứng minh nó đúng với n=k+1n=k+1
Viết lại đẳng thức cần chứng minh 13+23+33+...k3+(k+1)3=(1+2+3+4..+k+k+1)213+23+33+...k3+(k+1)3=(1+2+3+4..+k+k+1)2 (*)
Mặt khác ta có công thức tính tổng sau 1+2+3+4+...+n=n(n+1)21+2+3+4+...+n=n(n+1)2
⇒(1+2+3+4+...+n)2=(n2+n)24⇒(1+2+3+4+...+n)2=(n2+n)24
Vậy viết lại đẳng thức cần chứng minh
(k2+k)24+(k+1)3=(k2+3k+2)24(k2+k)24+(k+1)3=(k2+3k+2)24
⇔(k2+3k+2)2−(k2+k)2=4(k+1)3⇔(k2+3k+2)2−(k2+k)2=4(k+1)3
Bằng biện pháp "nhân tung tóe", đẳng thức cần chứng minh tuơng đuơng
⇔4k3+12k2+12k+4=4(k+1)3⇔4k3+12k2+12k+4=4(k+1)3
⇔4(k+1)3=4(k+1)3⇔4(k+1)3=4(k+1)3 ~ Đẳng thức này đúng.
Vậy theo nguyên lý quy nạp ta có đpcm.
3 tháng 3 2017
Giải hẳn hoi nha các bạn, đừng có viết luôn dạng tổng quát, nha 
VC
4
23 tháng 3 2017
Gọi \(ƯC\left(12n+1;30n+2\right)=d\)
\(\Rightarrow12n+1⋮d\Rightarrow60n+5⋮d\)
và \(30n+2⋮d\Rightarrow60n+ 4⋮d\)
Do đó \(60n+5-60n-4⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{12n+1}{30n+2}\) là phân số tối giản.
FT
23 tháng 3 2017
Gọi (12n+1),(30n+2) là d (1)
=>30n+2 \(⋮\) d
=> 2(30n + 2) \(⋮\) d hay 60n +4 \(⋮\) d
Tương tự ta chưng minh:
12n + 1 \(⋮\)d (2)
=> 5(12n+1) \(⋮\) d hay 60n +5 \(⋮\)d
Do đó (60n + 5) - ( 60n +4 ) \(⋮\)d hay 1 \(⋮\) d
=> d = 1 hoặc -1
Từ (1) và(2) ta có( 12n+1 ;30n+2) =1
=> P/s 12n + 1 /30n+2 là ps tối giản
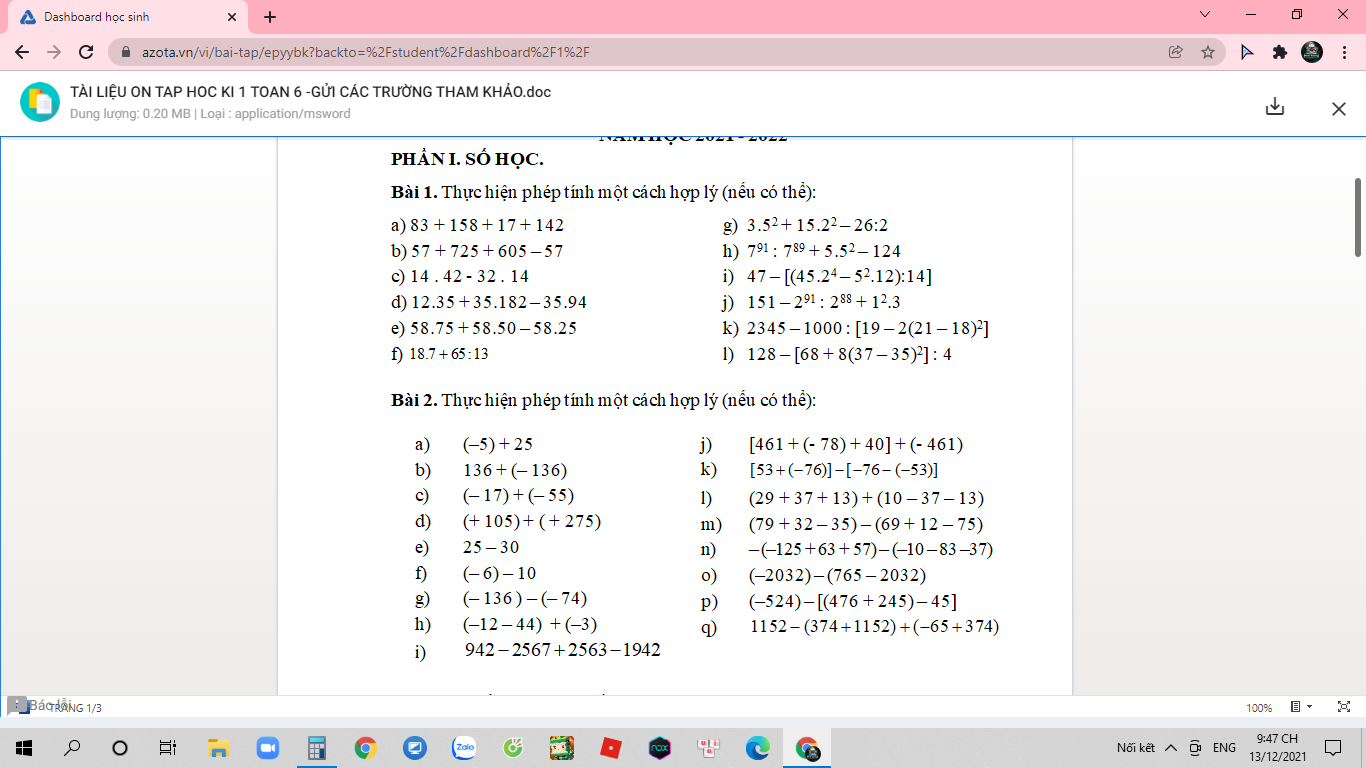
a) \(83+158+17+142.\)
\(=\left(83+17\right)+\left(158+142\right)\) \(=100+300=400.\)
b) \(\text{57 + 725 + 605 - 57}.\)
\(=\left(57-57\right)+\left(725+605\right)\) \(=1330.\)
c) \(14.42-32.14=14.\left(42-32\right)=14.10=140.\)
d) \(12.35+35.182-35.94=35\left(12+182-94\right)=35.100=3500.\)
e) \(58.75+58.50-58.25=58\left(75-25+50\right)=58.100=5800.\)