Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)

Bài 6
\(a,ĐK:x\ne\pm5\\ b,P=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\\ c,P=-3\Leftrightarrow\dfrac{1}{x+5}=-3\Leftrightarrow-3\left(x+5\right)=1\Leftrightarrow x=-\dfrac{16}{3}\\ \Leftrightarrow Q=\left(3x-7\right)^2=\left[3\cdot\left(-\dfrac{16}{3}\right)-7\right]^2=529\)
Bài 7:
\(a,ĐK:x\ne\pm3\\ b,P=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\\ b,P=4\Leftrightarrow4\left(x-3\right)=4\Leftrightarrow x=4\)

a) \(x^2+xy+x\)
\(=x\left(x+y+1\right)\)
Thay x=77, y=22
\(=77\left(77+22+1\right)\)
\(=77.100=7700\)
b) \(x\left(x-y\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(x-y\right)\)
\(=\left(x-y\right)^2\)
Thay x=53, y=3
\(=\left(53-3\right)^2\)
\(=50^2=2500\)
c) \(x\left(x-1\right)-y\left(1-x\right)\)
\(=\left(x+y\right)\left(x-1\right)\)
Thay x=2021, y=2029
\(=\left(2021+2019\right)\left(2021-1\right)\)
\(=4040.2020\)
\(=8160800\)

Những câu dạng như 19 hoặc 20 thì em nên sử dụng phương pháp trắc nghiệm chứ ko nên giải tự luận (vì như thế quá tồn thời gian, 1 bài kiểm tra trắc nghiệm ko đủ thời gian cho phép làm điều đó)
Câu 19 thử A, C đều sai, B cũng sai do ko phù hợp ĐKXĐ, do đó D đúng
Câu 20 tương tự, thử với \(x=-1\) thỏa mãn, \(x=3;x=4\) đều ko thỏa mãn, vậy A đúng
21A
22B
23A
24A
25C
26A
27C
28A

Bài 6:
a: Xét ΔHAD vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\)
Do đó: ΔHAD\(\sim\)ΔHBA
b: Ta có: ΔHAD\(\sim\)ΔHBA
nên HA/HB=HD/HA
hay \(HA^2=HB\cdot HD\)

\(\left(x^2-2x+3\right)\left(\frac{1}{2x}-5\right)\)
\(=\frac{x^2}{2x}-5x^2-\frac{2x}{2x}+10x+\frac{3}{2x}-15\)
\(=\frac{x^2}{2x}-5x^2-16+10x+\frac{3}{2x}\)
\(=-5x^2+\frac{x^2}{2x}+\frac{20x^2}{2x}+\frac{3}{2x}-16\)
\(=-5x^2+\frac{x^2+20x+3}{2x}-16\)
học tốt
(x^2-2x+3)(1/2x-5)=1/2x^3-5x^2-x^2+10x+3/2x-15=1/2x^3-6x^2+11,5x-15
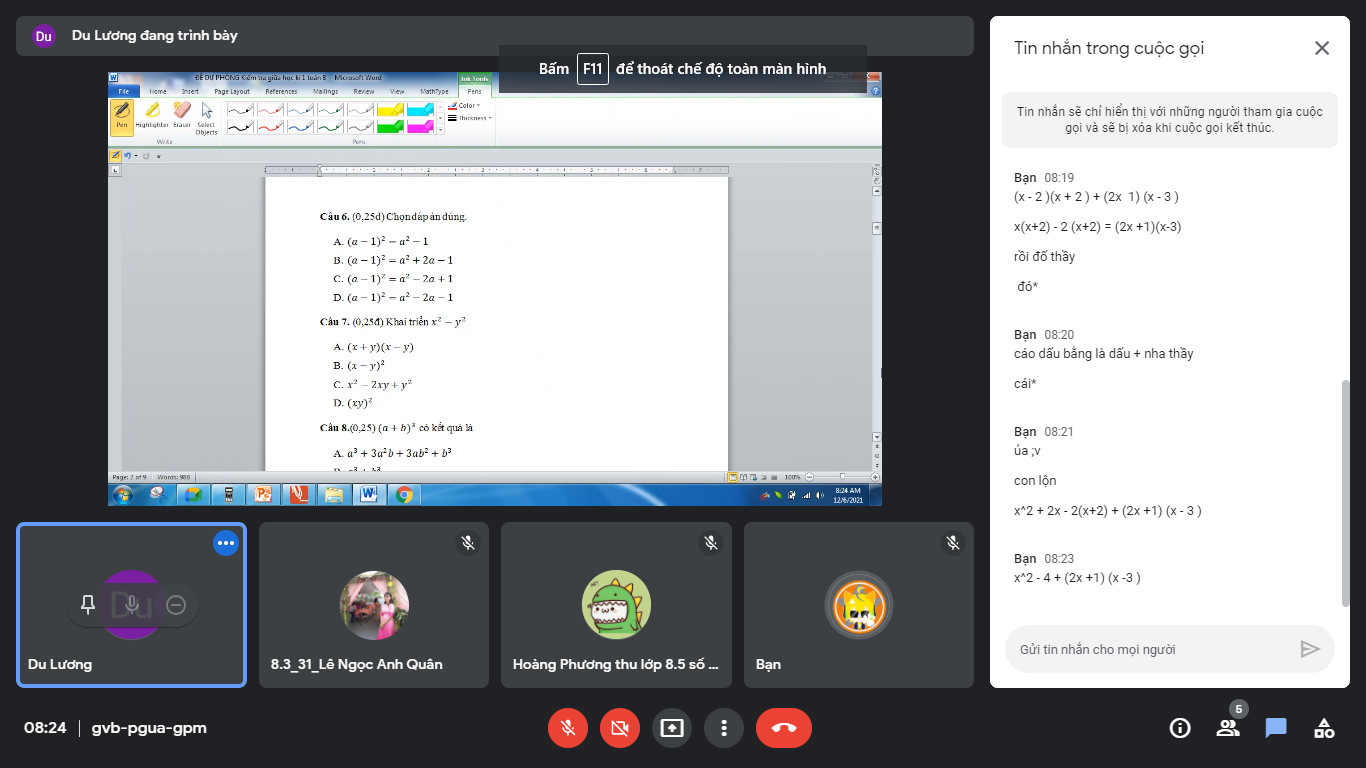 mong các anh chị giúp em làm bài tập làm câu đúng thôi nha anh chị cảm ơn anh chị nhiều.
mong các anh chị giúp em làm bài tập làm câu đúng thôi nha anh chị cảm ơn anh chị nhiều.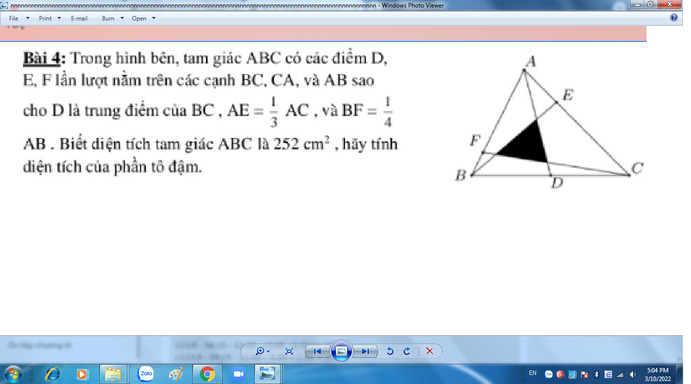
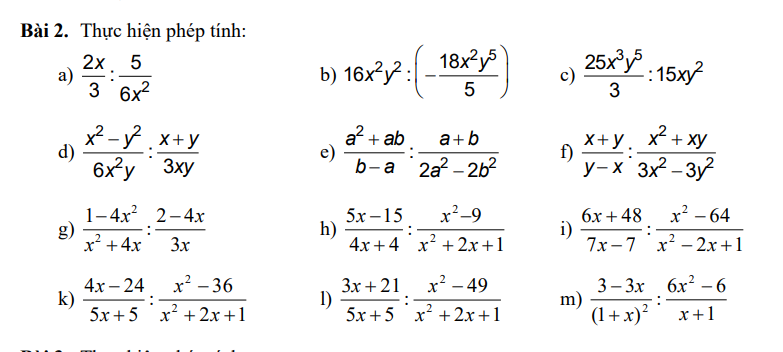




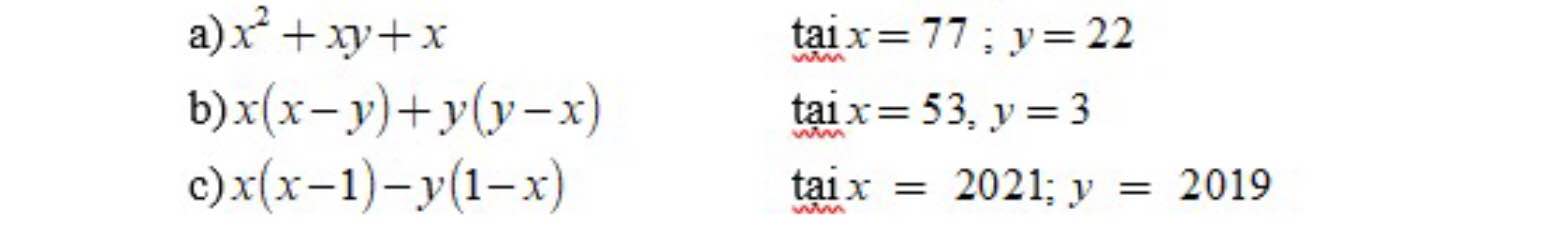 bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ

Câu 6: C
Câu 7: A
6.C
7.A
HT