Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)

#\(N\)
`a,` Xét Tam giác `MPH` và Tam giác `MQH` có:
`MP = MQ (g``t)`
`MH` chung
\(\widehat{MHP}=\widehat{MHQ}=90^0\)
`=>` Tam giác `MPH =` Tam giác `MQH (ch - cgv)`
`=>`\(\widehat{MPH}=\widehat{MQH}\) `( 2` góc tương ứng `)`
`b,` Vì Tam giác `MPH =` Tam giác `MQH (a)`
`=>` \(\widehat{PMH}=\widehat{QMH}\) `( 2` góc tương ứng `)`
`=> MH` là tia phân giác của \(\widehat{PMQ}\)
`c,` Ta có: \(\widehat{MPH}=\widehat{MQH}=50^0\) `(CMT)`
Xét Tam giác `MQH` có:
\(\widehat{MHQ}+\widehat{MQH}+\widehat{QMH}=180^0\) `(`đlí tổng `3` góc trong `1` tam giác `)`
\(90^0+50^0+\widehat{QMH}=180^0\)
`->`\(\widehat{QMH}=180^0-90^0-50^0=40^0\)

Bài 1:
Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
KA=KH
=>ΔBAK=ΔBHK
=>BA=BH
mà KA=KH
nên BK là trung trực của AH
=>BK vuông góc AH

Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)

Ta có:\(2009^{20}=\left(2009^2\right)^{10}=4036081^{10}< 20092009^{10}\)
Vậy \(2009^{20}< 20092009^{10}\)

Đổi 30 phút = 0,5 giờ
Quãng sông từ A đến B dài là:
\(x\) \(\times\) 0,5 + y \(\times\) 1 = 0,5\(x\) + y (km)
Kết luận Quãng đường từ A đên B dài: 0,5\(x\) + y (km)

Lời giải:
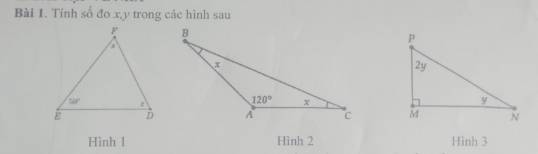
Áp dụng tính chất tổng 3 góc trong 1 tam giác bằng $180^0$
Hình 1: Hình không rõ ràng. Bạn xem lại.
Hình 2: $x+x+120^0=180^0$
$2x+120^0=180^0$
$2x=60^0$
$x=60^0:2=30^0$
Hình 3:
$2y+y+90^0=180^0$
$3y=180^0-90^0=90^0$
$y=90^0:3=30^0$
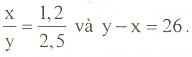
 x-2011
x-2011