
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
a, Ta có : \(x=4\Rightarrow\sqrt{x}=2\)
Thay vào biểu thức A ta được :
\(A=\frac{2+4}{4+4}=\frac{6}{8}=\frac{3}{4}\)
b, \(x\ge0;x\ne16\)
\(B=\frac{x}{x-16}-\frac{2}{\sqrt{x}-4}-\frac{2}{\sqrt{x}+4}\)
\(=\frac{x-2\sqrt{x}-8-2\sqrt{x}+8}{x-16}=\frac{x-4\sqrt{x}}{x-16}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}-4\right)}{\left(\sqrt{x}\pm4\right)}=\frac{\sqrt{x}}{\sqrt{x}+4}\)
c, Ta có : \(C=A.B=\frac{\sqrt{x}}{\sqrt{x}+4}.\frac{\sqrt{x}+4}{x+4}=\frac{\sqrt{x}}{x+4}\le0\)
Dấu ''='' xảy ra khi \(x=0\)( em ko chắc ý c lắm vì cũng chưa gặp bh )
trình bày như này thì khi thế x vào mẫu nó là 0 nên băn khoăn :)
\(x+4\le0\)do \(\sqrt{x}\ge0\)\(\Leftrightarrow x\le-4\)
Ta dễ thấy điểm rơi đạt tại \(x=2;y=3;z=4\)
Áp dụng bất đẳng thức AM-GM :
\(A=\left(\frac{3}{x}+\frac{3x}{4}\right)+\left(\frac{9}{2y}+\frac{y}{2}\right)+\left(\frac{4}{z}+\frac{z}{4}\right)+\frac{1}{4}\left(x+2y+3z\right)\)
\(\ge2\left(\frac{3}{2}+\frac{3}{2}+1\right)+\frac{1}{4}.20=13\)
Vậy Min A = 13 <=> x = 2 ; y = 3 ; z = 4

Bài 5
\(a - b = 2 <=> b = a - 2\)
Do đó: \(P = 3a^2 + (a-2)^2 + 8\)
\(= 3a^2 + a^2 - 4a + 4 + 8\)
\(= 4a^2 - 4a + 12\)
\(= (2a - 1)^2 + 11\)
Vì \((2a - 1)^2 \geq 0 \) với mọi a nên \(= (2a - 1)^2 + 11 \geq 11 \) hay \(P \geq 11\)
Dấu "=" xảy ra \(\begin{cases} a - b = 2 \\ 2a - 1 = 0 \\\end{cases} <=> \begin{cases} a = \dfrac{1}{2} \\ b = -\dfrac{3}{2} \\\end{cases}\)
Vậy giá trị nhỏ nhất của P là 11 tại \(\begin{cases} a = \dfrac{1}{2} \\ b = -\dfrac{3}{2} \\\end{cases}\)
câu hình:
a) Vì AB là đường kính \(\Rightarrow\angle ADB=90\Rightarrow\angle EDB+\angle EHB=180\)
\(\Rightarrow EDHB\) nội tiếp
b) Xét \(\Delta AHE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle DABchung\\\angle AHE=\angle ADB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AHE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AH}{AD}=\dfrac{AE}{AB}\Rightarrow AB.AH=AD.AE\)
mà \(AH.AB=AC^2\) (hệ thức lượng) \(\Rightarrow AC^2=AD.AE\)
c) Vì \(EF\parallel AB\) \(\Rightarrow\angle CFE=\angle CBA=\angle CDA=\angle CDE\)
\(\Rightarrow CDFE\) nội tiếp mà \(\angle CEF=90\) \((EF\parallel AB,AB\bot CH)\)
\(\Rightarrow\angle CDF=90\Rightarrow CD\bot DF\)
Vì \(\Delta CDF\) vuông tại D có K là trung điểm CF \(\Rightarrow KC=KD\)
\(\Rightarrow\Delta KCD\) cân tại K \(\Rightarrow\angle DKB=2\angle DCB=2\angle DAB=\angle DOB\)
\(\Rightarrow DKOB\) nội tiếp \(\Rightarrow K\in\left(OBD\right)\)


à nhon mik thiếu
Cho a > 0; b > 0; c > 0
Chứng minh bất đẳng thức: ![]()

arigato mk đang ôn thi mk đang học lớp 9 sắp thi 10 r hông bít ang năm thi thế nào nữa

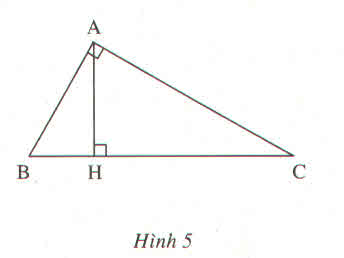
a,Trong \(\Delta\) ABH có AHB=900 (BH \(\perp\) BC tại H -gt)
AH2 + BH2 =AB2 (định lý Pi-ta-go)
T/s:162 +252 =AB2
\(\Rightarrow\) AB2 =881
mà AB>0
\(\Rightarrow\) AB=\(\sqrt{881}\)\(\approx\) 29.68
Trong\(\Delta\) ABC có BAC=900 (gt), Đường cao AH (gt)
AH2= BH*CH (hệ thức lượng)
T/s: 162=25*CH
\(\Rightarrow\) CH=\(\dfrac{16^2}{25}\) = 10.24
Có:BH+HC=BC(H\(\in\) BC)
T/s: 25+10.24=BC
\(\Rightarrow\) BC=35.24
Trong \(\Delta\) ABC có:BAC=900 (GT)
AB2 +AC2 =BC2(Định lý Py-ta-go)
T/s:29.682+AC2\(\approx\)35.242
\(\Rightarrow\) AC2\(\approx\)35.242-29.682
\(\approx\)360.95
Mà AC>0
\(\Rightarrow\) AC\(\approx\) 19

Gọi x là số học sinh dự thi vào lớp 10 của trường A (h/s, \(x\in N\), \(0< x< 435\))
y là số học sinh dự thi vào lớp 10 của trường B (h/s, \(y\in N\), \(0< y< 435\))
Vì hai trường A và B có 435 học sinh dự thi nên ta có PT: \(x+y=435\) (1)
Vì trường A có tỉ lệ thi đỗ vào lớp 10 là 85%, trường B có tỉ lệ thi đỗ vào lớp 10 là 90%, và cả hai trường có tỉ lệ thi đỗ vào lớp 10 là 87% nên ta có PT: \(85\%x+90\%y=87\%\cdot435\) (2)
Từ (1) và (2), ta có HPT: \(\hept{\begin{cases}x+y=435\\85\%x+90\%y=87\%\cdot435\end{cases}}\)
Giải HPT, ta có: \(\hept{\begin{cases}x=261\\y=174\end{cases}}\) (TMĐK)
Vậy trường A có 261 học sinh dự thi và trường B có 174 học sinh dự thi, vào lớp 10.
Gọi x là số học sinh dự thi vào lớp 10 của trường A (h/s, \(x\in N\),\(0< x< 500\))
y là số học sinh dự thi vào lớp 10 của trường B (h/s, \(y\in N\),\(0< y< 500\))
Vì cả hai trường có 435 thi đỗ vào lớp 10 đạt tỉ lệ là 87% nên ta có PT: \(x+y=\frac{435}{87\%}\) <=> \(x+y=500\) (1)
Vì trường A có tỉ lệ thi đỗ vào lớp 10 là 85%, trường B có tỉ lệ thi đỗ vào lớp 10 là 90%, và cả hai trường có 435 học sinh thi đỗ vào lớp 10 nên ta có PT: \(85\%x+90\%y=435\) (2)
Từ (1) và (2), ta có HPT: \(\hept{\begin{cases}x+y=500\\85\%x+90\%y=435\end{cases}}\)
Giải HPT, ta có: \(\hept{\begin{cases}x=300\\y=200\end{cases}}\) (TMĐK)
Vậy trường A có 300 học sinh dự thi và trường B có 200 học sinh dự thi, vào lớp 10.







chịu thua
em hc lớp 6