
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)

- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)

- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.

a)
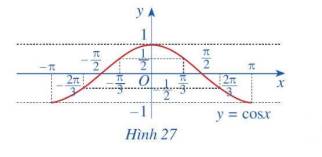
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
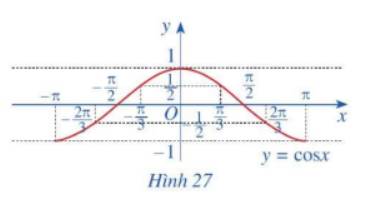
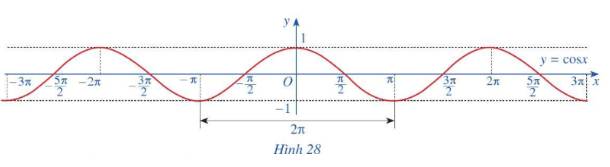
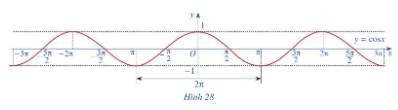
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

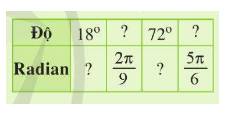
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
Độ | \({18^ \circ }\) | \(\frac{{2\pi }}{9}.\frac{{180}}{\pi } = {40^ \circ }\) | \({72^ \circ }\) | \(\frac{{5\pi }}{6}.\frac{{180}}{\pi } = {150^ \circ }\) |
Radian | \(18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\) | \(\frac{{2\pi }}{9}\) | \(72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\) | \(\frac{{5\pi }}{6}\) |

Trong Hình 4b, góc lượng giác là (Oz,Ot) với tia đầu là tia Oz và tia cuối là tia Ot

Mẫu số liệu được chia thành 7 nhóm:
- Có 6 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 15 đến dưới 20 phút.
- Có 14 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 20 đến dưới 25 phút.
- Có 25 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 25 đến dưới 30 phút.
- Có 37 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 30 đến dưới 35 phút.
- Có 21 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 35 đến dưới 40 phút.
- Có 13 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 40 đến dưới 45 phút.
- Có 9 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 45 đến dưới 50 phút.
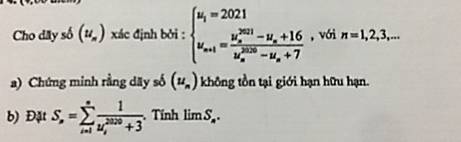




.png)






a) Xét hàm \(f\left(x\right)=\dfrac{x^{2021}-x+16}{x^{2020}-x+7}\)
\(f\left(x\right)-4=\dfrac{x^{2021}-x+16-4x^{2020}+4x-28}{x^{2020}-x+7}\)
\(=\dfrac{x^{2021}-4x^{2020}+3x-12}{x^{2020}-x+7}\)
\(=\dfrac{\left(x^{2020}+3\right)\left(x-4\right)}{\left(x^{2020}+3\right)-\left(x-4\right)}\)
Vậy nếu \(x>4\) thì \(f\left(x\right)-4>0\Leftrightarrow f\left(x\right)>4\).
Ta có \(u_1>4\) \(\Rightarrow u_2=f\left(u_1\right)>4\) \(\Rightarrow u_3=f\left(u_2\right)>4\) và cứ như thế, ta thu được \(u_n>4,\forall n\)
Mặt khác, xét hiệu \(f\left(x\right)-x\), ta có \(f\left(x\right)-x\)
\(=\dfrac{x^{2021}-x+16}{x^{2020}-x+7}-x\)
\(=\dfrac{x^{2021}-x+16-x^{2021}+x^2-7x}{x^{2020}-x+7}\)
\(=\dfrac{x^2-8x+16}{x^{2020}-x+7}\)
\(=\dfrac{\left(x-4\right)^2}{x^{2020}-x+7}>0\)
\(\Rightarrow f\left(x\right)>x\)
\(\Rightarrow u_{n+1}=f\left(u_n\right)>u_n,\forall n\)
\(\Rightarrow\left(u_n\right)\) là dãy tăng.
Giả sử \(\left(u_n\right)\) bị chặn trên. Khi đó đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L>2021\). Khi đó:
\(L=\dfrac{L^{2021}-L+16}{L^{2020}-L+7}\)
\(\Leftrightarrow L^{2021}-L^2+7L=L^{2021}-L+16\)
\(\Leftrightarrow L^2-8L+16=0\)
\(\Leftrightarrow L=4\), vô lý.
Vậy \(\left(u_n\right)\) không bị chặn trên \(\Rightarrow\lim\limits_{n\rightarrow+\infty}u_n=+\infty\) hay \(\left(u_n\right)\) không có ghhh.
b) Ta có \(\dfrac{1}{f\left(x\right)-4}=\dfrac{\left(x^{2020}+3\right)-\left(x-4\right)}{\left(x^{2020}+3\right)\left(x-4\right)}\)
\(=\dfrac{1}{x-4}-\dfrac{1}{x^{2020}+3}\)
Từ đó ta có \(\dfrac{1}{u_{n+1}-4}=\dfrac{1}{u_n-4}-\dfrac{1}{u_n^{2020}+3}\)
\(\Leftrightarrow\dfrac{1}{u_n^{2020}+3}=\dfrac{1}{u_n-4}-\dfrac{1}{u_{n+1}-4}\)
\(\Rightarrow S_n=\sum\limits^n_{i=1}\dfrac{1}{u_i^{2020}+3}=\dfrac{1}{u_1-4}-\dfrac{1}{u_{n+1}-4}\)
\(=\dfrac{1}{2017}-\dfrac{1}{u_{n+1}-4}\)
\(\Rightarrow\lim\limits_{n\rightarrow+\infty}S_n=\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{2017}-\dfrac{1}{u_{n+1}-4}\right)=\dfrac{1}{2017}\)
(vì \(\lim\limits_{n\rightarrow+\infty}u_n=+\infty\))
Vậy \(\lim\limits_{n\rightarrow+\infty}S_n=\dfrac{1}{2017}\)