Question

[Phượng Phạm]

ccau giúp tớ vs, nhanh nha, chi tiết nx

Answer 1

[『Kuroba ム Tsuki Ryoo ︵²ᵏ⁷』]

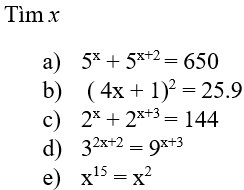
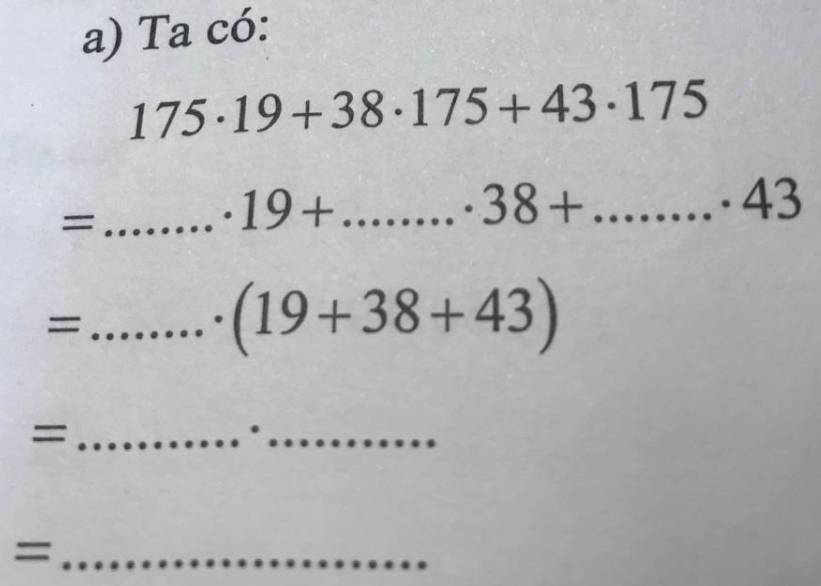
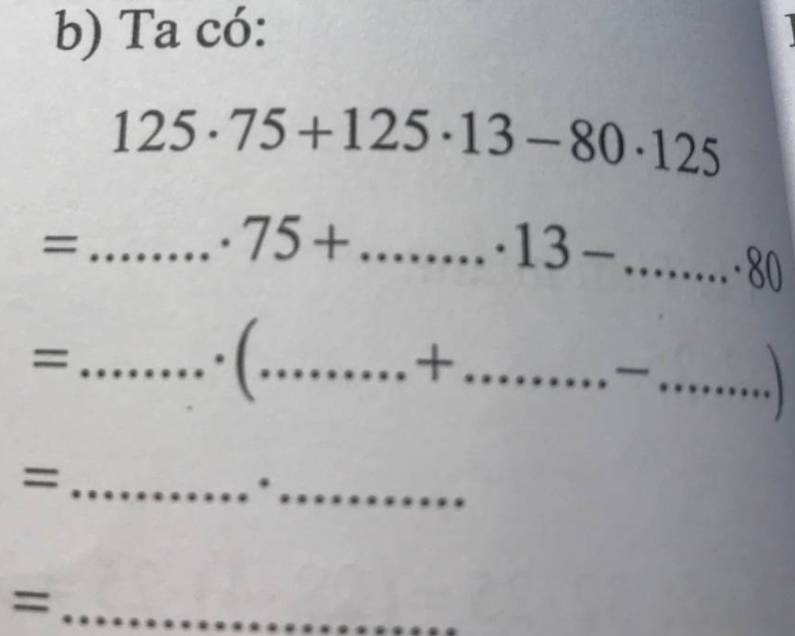
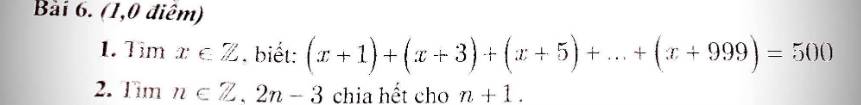
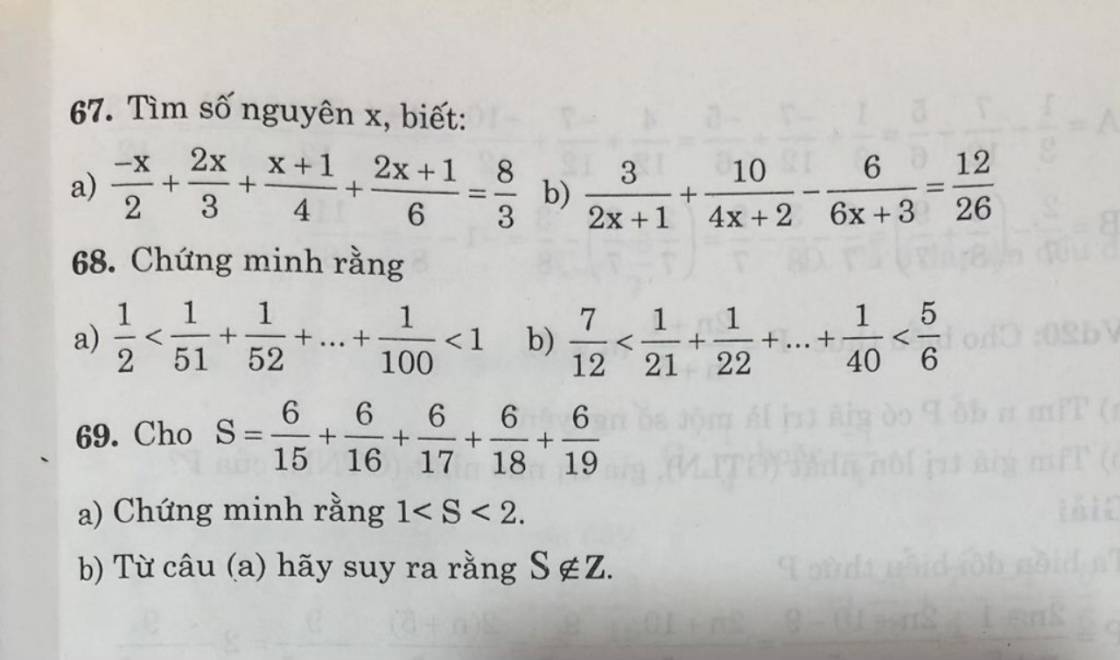
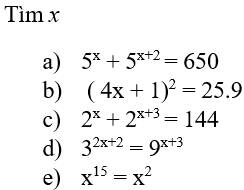
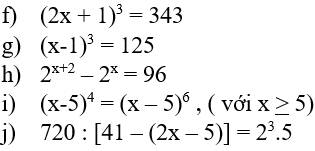
`@` `\text {Ans}`

`\downarrow`

`a)`

\(5^x+5^{x+2}=650\)

`\Rightarrow 5^x + 5^x . 5^2 = 650`

`\Rightarrow 5^x . (1 + 5^2) = 650`

`\Rightarrow 5^x . 26 = 650`

`\Rightarrow 5^x = 650 \div 26`

`\Rightarrow 5^x = 25`

`\Rightarrow 5^x = 5^2`

`\Rightarrow x = 2`

Vậy, `x = 2`

`b)`

`(4x + 1)^2 = 25.9`

`\Rightarrow (4x + 1)^2 = 225`

`\Rightarrow (4x + 1)^2 = (+-15^2)`

`\Rightarrow`\(\left[{}\begin{matrix}4x-1=15\\4x-1=-15\end{matrix}\right.\)

`\Rightarrow `\(\left[{}\begin{matrix}4x=16\\4x=-14\end{matrix}\right.\)

`\Rightarrow `\(\left[{}\begin{matrix}x=4\\x=-\dfrac{7}{2}\end{matrix}\right.\)

Vậy, `x \in`\(\left\{-\dfrac{7}{2};4\right\}\)

`c)`

\(2^x+2^{x+3}=144\)

`\Rightarrow 2^x + 2^x . 2^3 = 144`

`\Rightarrow 2^x . (1 + 2^3) = 144`

`\Rightarrow 2^x . 9 = 144`

`\Rightarrow 2^x = 144 \div 9`

`\Rightarrow 2^x = 16`

`\Rightarrow 2^x = 2^4`

`\Rightarrow x = 4`

Vậy, `x = 4`

`d)`

\(3^{2x+2}=9^{x+3}\)

`\Rightarrow `\(3^{2x+2}=\left(3^2\right)^{x+3}\)

`\Rightarrow `\(3^{2x+2}=3^{2x+6}\)

`\Rightarrow 2x + 2 = 2x + 6`

`\Rightarrow 2x - 2x = 6 - 2`

`\Rightarrow 0 = 4 (\text {vô lý})`

Vậy, `x` không có giá trị nào thỏa mãn.

`e)`

\(x^{15}=x^2\)

`\Rightarrow `\(x^{15}-x^2=0\)

`\Rightarrow `\(x^2\cdot\left(x^{13}-1\right)=0\)

`\Rightarrow `\(\left[{}\begin{matrix}x^2=0\\x^{13}-1=0\end{matrix}\right.\)

`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x^{13}=1\end{matrix}\right.\)

`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Vậy, `x \in`\(\left\{0;1\right\}.\)