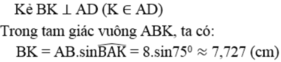Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

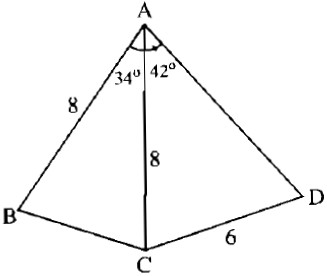
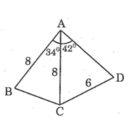
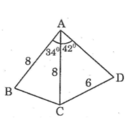
a) Kẻ AM vuong goc voi BC tai M
Tam giac BAC can tai A, co AM la duong cao=> AM cung la trung tuyen va phan giac cua tam giac ABC => MB=MC va goc BAM = goc CAM = 34/2=17 do
Xet tam giac AMB vuong tai M, ta co:
sin BAM = BM/AB => BM = AB.sinBAM = 8.sin(17 do)
Suy ra BC= 2.BM = 16.sin(17 do)
b) Ve CH vuong goc voi AD tai H
Xet tam giac AHC vuong tai H co:
sinCAD = CH/AC => CH= AC.sinCAD=8.sin(42 do)
Xet tam giac CHD vuong tai H co:
sin ADC = CH/CD = 8.sin(42 do)/6 => goc ADC = ( bam may tinh)
c) Ve BK vuong goc voi AD tai K( K nam giua A,D), nhu vay khoang cach tu B den AD chinh la BK
goc BAD= goc BAC + goc CAD = 34 +42 = 76 do
Xet tam giac AKB vuong tai K, ta co:
sinBAD = BK./AB => BK =AB. sinBAD = 8.sin(72 do)
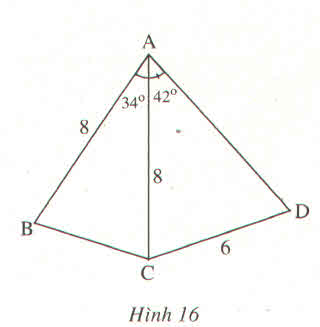
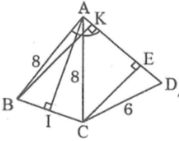
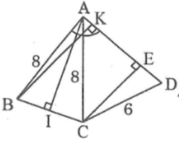
a)Kẻ đường cao AH
Ta có AB = AC => tam giác ABC cân tại A
Nên đường cao AH vừa là phân giác, vừa là trung trực
Suy ra BAHˆBAH^ = CAHˆCAH^ = BACˆ2BAC^2 = 34023402 = 170170
Xét tam giác AHC vuông tại H, ta có:
sin CAHˆCAH^ = HCACHCAC => HC = sin CAHˆCAH^.AC = sin 170170.8 = 2,34
Do AH là trung trực của tam giác ABC nên BC = 2HC = 2.2,34 = 4,68
Vậy BC = 4,68cm
b) Kẻ CE vuông góc với AD
Xét tam giác ACE vuông tại E, ta có:
ADEˆADE^ = CEACCEAC => CE = sin CAEˆCAE^.AC = sin 420ˆ420^.8 = 5,353
Xét tam giác CED vuông tại E, ta có
sin CDEˆCDE^ = CECDCECD = 5,35365,3536 ≈≈ 0,8922
Suy ra CDEˆCDE^ = 63,15063,150 = 6306309'
Hay ADCˆADC^ = 63,15063,150
c) Ta có BADˆBAD^ = BACˆBAC^ + CADˆCAD^ = 340340 + 420420 = 760760
Kẻ BF vuông góc với AD
Xét tam giác BFA vuông tại F, ta có
BF = sin BADˆBAD^.AB = sin 760760.8 = 7,76
Vậy khoảng cách từ điểm B đến cạnh AD bằng 7,76cm

Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(cos35=\dfrac{8^2+8^2-BC^2}{2\cdot8\cdot8}\)
=>\(128-BC^2=2\cdot64\cdot cos35=128\cdot cos35\)
=>\(BC=\sqrt{128-128\cdot cos35}\simeq4,81\left(cm\right)\)
Xét ΔADC có \(\dfrac{CD}{sinCAD}=\dfrac{AC}{sinADC}\)
=>\(\dfrac{8}{sinADC}=\dfrac{6}{sin43}\)
=>\(sinADC=8\cdot\dfrac{sin43}{6}\simeq0,91\)
=>\(\widehat{ADC}\simeq65^0\)

a:
ΔABC cân tại A
=>góc ABC=góc ACB=(180-34)/2=146/2=73 độ
Xét ΔABC có BC/sinA=AB/sinC=AC/sinB=2R
=>BC/sin34=8/sin73
=>\(BC\simeq4,68\left(cm\right)\)
b: Xét ΔADC có \(cosCAD=\dfrac{AC^2+AD^2-CD^2}{2\cdot AC\cdot AD}\)
=>\(8^2+10.6^2-CD^2=2\cdot8\cdot10.6\cdot cos42\)
=>\(CD\simeq7,09\left(cm\right)\)
Xét ΔACD có
\(\dfrac{AC}{sinADC}=\dfrac{CD}{sinCAD}\)
=>8/sinADC=7,09/sin42
=>\(sinADC\simeq0,76\)
=>\(\widehat{ADC}\simeq49^0\)
c:
góc DAB=góc DAC+góc BAC
=42+34
=76 độ
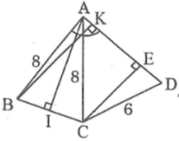
Kẻ BH vuông góc AD
=>BH=d(B;AD)
Xét ΔBHA vuông tại H có
sinHAB=BH/BA
=>BH/8=sin76
=>\(BH\simeq7,76\left(cm\right)\)

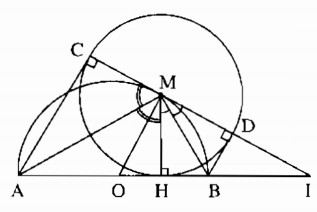
A B M H O C D I
a) Áp dụng tính chất hai tiếp tuyến giao nhau: ^HMC = 2.^AMH; ^HMD = 2.^BMH
Suy ra ^HMC + ^HMB = 2(^AMH + ^BMH) = 1800 => 3 điểm C,M,D thẳng hàng (đpcm).
Có C,M,D thẳng hàng, Do C,D thuộc (M;MH) nên CD là đường kính của (M;MH)
Khi đó MO là đường trung bình của hình thang vuông ACDB => MO // AC // BD
=> MO vuông góc CD => CD là tiếp tuyến của (O) (đpcm).
b) Dễ thấy AC + BD = AH + BH = 2R (R là bán kính của (O)) (không đổi).
c) Áp dụng hệ thức lượng trong tam giác vuông IMO có OH.OI = OM2 = R2 (không đổi).