Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A=m^6-6m^5+10m^4+m^3+98m-26\)
\(=m^6-m^4+m^3-6m^5+6m^3-6m^2+11m^4-11m^2+11m-6m^3+6m-6+17m^2+81m-20\)
\(=m^3-6m^2+11m-6+\dfrac{17m^2+81m-20}{m^3-m+1}\)
b: \(C=m^3-6m^2+11m-6=\left(m-1\right)\left(m-3\right)\left(m-2\right)\) luôn chia hết cho 6
b: Để đa thức dư bằng 0 thì 17m^2+81m-20=0
=>m=-5 hoặc m=4/17

Bài 4:
=>x(x^2+1)=0
=>x=0
Bài 5:
=>\(3n^3+n^2+9n^2-1-4⋮3n+1\)
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Bài 3:
\(a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)

Bài 2:
a: =x^2+x+1/4+3/4
=(x+1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=-1/2
b: =-(x^2-x-2)
=-(x^2-x+1/4-9/4)
=-(x-1/2)^2+9/4<=9/4
Dấu = xảy ra khi x=1/2
c: =x^2-4x+4-3
=(x-2)^2-3>=-3
Dấu = xảy ra khi x=2

Bài 3:
\(\dfrac{f\left(x\right)}{g\left(x\right)}=\dfrac{x^4+ax^2+b}{x^2-3x+2}\)
\(=\dfrac{x^4-3x^3+2x^2+3x^3-9x^2+6x+\left(a+7\right)x^2-3x\left(a+7\right)+2\left(a+7\right)+x\left(-6+3a+7\right)+b-2a-14}{x^2-3x+2}\)
Để đây là phép chia hết thì 3a+1=0 và b-2a-14=0
=>a=-1/3; b=2a+14=-2/3+14=40/3

Bài 1: a,\(y^3-10y^2+25y=y\left(y^2-10y+25\right)\)
=\(y\left(y-5\right)^2\)
b,\(3x^2-6xy+3y^2-12z^2=3\left(x^2-2xy+y^2-4z^2\right)\)
=\(3\left[\left(x-y\right)^2-\left(2z\right)^2\right]=3\left(x-y+2z\right)\left(x-y-2z\right)\)
Bài 2:\(x^2-4x+5=\left(x^2-4x+4\right)+1\)
=\(\left(x-2\right)^2+1\)
Vì \(\left(x-2\right)^2\ge0\)với mọi x
Nên \(\left(x-2\right)^2+1\ge1\)với mọi x
Do đó GTNN của A =1 \(\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)

Bài 1 :
a)Tìm giá trị nhỏ nhất của biểu thức
A = 2x2 - 4x + 8
\(=\left(\sqrt{2}x\right)^2-2.\sqrt{2}x.\sqrt{2}+\left(\sqrt{2}\right)^2+4\)
\(=\left(\sqrt{2}x+\sqrt{2}\right)^2+4\)
Ta có : \(\left(\sqrt{2}x+\sqrt{2}\right)^2\ge0\) \(\Rightarrow\left(\sqrt{2}x+\sqrt{2}\right)^2+4\ge4>0\)
=> A > 4
=> Amin = 4 \(\Leftrightarrow\left(\sqrt{2}x+\sqrt{2}\right)^2=0\)
\(\Leftrightarrow\sqrt{2}x+\sqrt{2}=0\)
\(\Leftrightarrow x=-1\)
Bài 1:
a) \(A=2x^2-4x+8\)
\(=2\left(x^2-2x+4\right)=2\left(x-2\right)^2\)
Xét \(2\left(x-2\right)^2\ge0\)
\(\Rightarrow Min_A=0\Leftrightarrow x=2\)
b) \(B=n^5-5n^3+4n\)
\(=n\left(n^4-5n^2+4\right)\)
\(=n\left(n^4-n^2-4n^2+4\right)\)
\(=n\left[n^2\left(n^2-1\right)-4\left(n^2-1\right)\right]\)
\(=n\left[\left(n^2-4\right)\left(n^2-1\right)\right]\)
\(=n\left[\left(n-2\right)\left(n+2\right)\left(n-1\right)\left(n+1\right)\right]\)
\(=\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\)
Xét \(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\) là 5 số nguyên liên tiếp
\(\Rightarrow\)\(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)⋮2;3;4;5\)
\(\Rightarrow\)\(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)⋮120\)
\(\Rightarrow\)\(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)⋮30\)
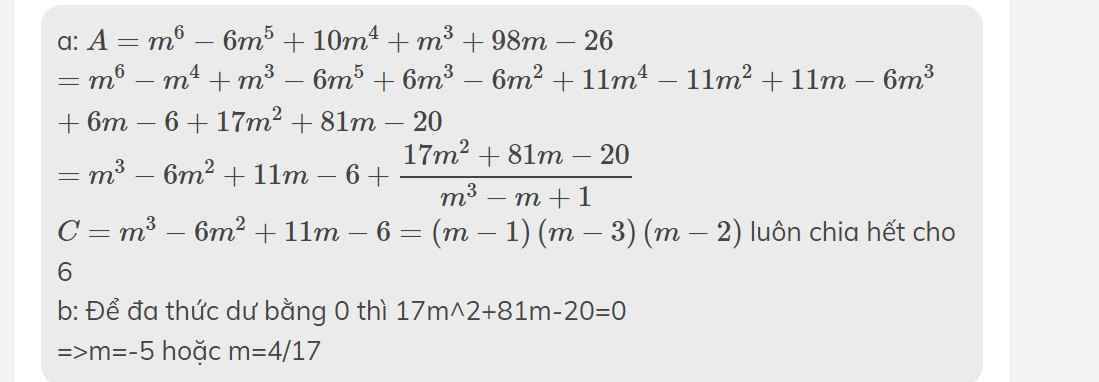



a: \(A=m^6-6m^5+10m^4+m^3+98m-26\)
\(=m^6-m^4+m^3-6m^5+6m^3-6m^2+11m^4-11m^2+11m-6m^3+6m-6+17m^2+81m-20\)
\(=m^3-6m^2+11m-6+\dfrac{17m^2+81m-20}{m^3-m+1}\)
\(C=m^3-6m^2+11m-6=\left(m-1\right)\left(m-3\right)\left(m-2\right)\) luôn chia hết cho 6
b: Để đa thức dư bằng 0 thì 17m^2+81m-20=0
=>m=-5 hoặc m=4/17