
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đây là dạng toán viết phương trình tiếp tuyến tại một điểm A(a,b)
ta là như sau:
bước 1: tính y'
bước 2: tính y'(a)
bước 3: áp dụng công thức y=y'(a)(x-a)+b
áp dụng vào bài trên ta có
\(y'=3x^2-3\)
\(y'\left(0\right)=-3\)
vậy phương trình tiếp tuyến của đồ thị có dạng
\(y=-3\left(x-0\right)+\left(-1\right)=-3x-1\)

vì đồ thị hàm số đi qua điểm \(A\left(-1;\frac{5}{2}\right)\) nên tọa độ của A thỏa mãn phương trình sau: \(\frac{a+b}{-2}=\frac{5}{2}\Rightarrow a+b=-5\)(*)
ta tính y' có:
\(y'=\frac{\left(2ax-b\right)\left(x-1\right)-\left(ax^2-bx\right)}{\left(x-1\right)^2}=\frac{2ax^2-2ax-bx+b-ax^2+bx}{\left(x-1\right)^2}=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\)
vì hệ số góc của tiếp tuyến tại điểm O(0;0) bằng 3 nên \(y'\left(O\right)=\frac{b}{\left(0-1\right)^2}=-3\Rightarrow b=-3\)
thay b=-3 vào (*) ta tìm được a=-2
vậy a=-2;b=-3

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k

ta tính \(y'=3x^2\)
để tiếp tuyến của đồ thị hàm số song song với đường thẳng \(y=-3x+1\) thì \(y'\left(x_0\right)=\frac{-1}{-3}=\frac{1}{3}\) giả pt suy ra đc \(x_0=\pm\frac{1}{3}\)
TH1: \(x_0=\frac{1}{3}\) suy ra \(y_0=\frac{1}{27}+1=\frac{28}{27}\)
vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x-\frac{1}{3}\right)+\frac{28}{27}=\frac{1}{3}x+\frac{25}{27}\)
TH2:\(x_0=-\frac{1}{3}\) suy ra \(y_0=-\frac{1}{27}+1=\frac{26}{27}\)
vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x+\frac{1}{3}\right)+\frac{26}{27}=\frac{1}{3}x+\frac{29}{27}\)

a) vẽ dễ lắm ; tự vẽ nha
b) xét phương trình hoành độ của 2 đồ thị đó
ta có : \(x^2=-2x+3\Leftrightarrow x^2+2x-3=0\)
ta có : \(a+b+c=1+2-3=0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=1\) \(\Rightarrow y=x^2=1^2=1\) vậy \(A\left(1;1\right)\)
\(x_2=\dfrac{c}{a}=-3\) \(\Rightarrow y=x^2=\left(-3\right)^2=9\) vậy \(B\left(-3;9\right)\)
vậy 2 đồ thị cắt nhau tại 2 điểm phân biệt là \(A\left(1;1\right)\) và \(B\left(-3;9\right)\)

Đáp án A.
Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x0 là ![]()
Cách giải: TXĐ: D = R
Ta có 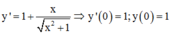
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 0 là: ![]()

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Đáp án là B.
Đạo hàm: y ' = 9 x 2 − 2 x − 7 .
Phương trình tiếp tuyến tại điểm M x 0 ; y 0 là : y = k x − x 0 + y 0 .
Hệ số góc k = y ' 0 = − 7
Phương trình tiếp tuyến cần tìm tại điểm A 0 ; 1 là: y = − 7 x − 0 + 1 ⇔ y = − 7 x + 1