Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
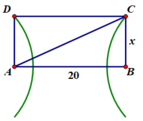
Để S hình chữ nhật ABCD nhỏ nhất và C, D đều nằm trên đường cực đại thì C và D phải nằm trên 2 đường cực đại gần nguồn nhất.
Có
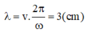
Số đường cực đại trên AB:
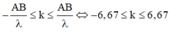
Để C là cực đại gần nguồn nhất thì k = 6.
Suy ra
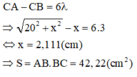

Chọn đáp án A
+ Để diện tích ABCD nhỏ nhất thì C và D phải nằm trên hai cực đại ngoài cùng.
Xét các đường cực đại ta có: ![]()
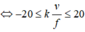
![]()
![]()
Vậy D nằm trên cực đại ứng với ![]()
Tam giác ABD vuông tại A nên ta có:
![]()
![]()
![]()
![]()

Đáp án B
Ta có :
![]()
Trên AB , dao động cực đại gần A ( hoặc B ) nhất là :
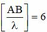
Để điện tích hình chữ nhật nhỏ nhất , CD nằm trên cực đại ứng với k = 6 và k = -6
Tại điểm D :
![]()
![]()
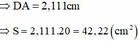

Đáp án A
Vì AB không đổi nên để diện tích HCN ABCD min thì BC phải min, tức là C phải là cực đại gần B nhất. Có λ = 3 cm.


ta có:f=4p/2p=2(hz)
lamda=v/f=50/2=25(cm)
vì M cùng pha với O nên :2p*d1/lamda=2p suy ra d1=25(cm)
vì N ngược pha với O nên :2p*d2/lamda=p suy ra d2 =12.5(cm)

Dòng điện xoay chiều khiến cho dây chịu tác dụng của lực từ, và sẽ dao động theo phương vuông góc với đường sức từ, với tần số 50Hz, hay ω=2πf=100πω=2πf=100π và T=0.02sT=0.02s
Khoảng cách giữa 2 điểm dừng (ứng với 1 bụng sóng) là λ/2=vT/2=12×0.02/2=0.12λ/2=vT/2=12×0.02/2=0.12
Có 6 bụng sóng, vậy thì chiều dài sợi dây là: 6λ2=0.12×6=0.72(m)6λ2=0.12×6=0.72(m)
Đáp án là A. 72cm

Ta có: \(\dfrac{\pi x}{4}=\dfrac{2\pi x}{\lambda}\Rightarrow \lambda = 8cm\)
Chu kì: \(T=1s\)
Tốc độ truyền sóng: \(v=\dfrac{\lambda}{T}=8cm/s\)

+ Bước sóng:
+ Diện tích nhỏ nhất khi C và D gần AB nhất.
+ vậy C và D phải thuộc hai cực đại ngoài cùng của AB.
+ Số cực đại trên AB được xác định bởi:
+ vậy diện tích hình chữ nhật ABCD nhỏ nhất là:
=> Chọn C.