Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

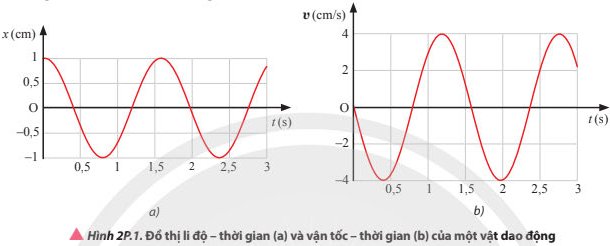
Từ đồ thị ta xác định được A = 1cm
Ta có: vmax = ωA⇒ω = 4 (rad/s)
Phương trình li độ của dao động: x = cos(4t) (cm)
Phương trình vận tốc của dao động: v = 4cos(4t+\(\frac{\pi }{2}\)) (cm/s)
Phương trình gia tốc của vật dao động: a = 16cos(4t) (m/s2)

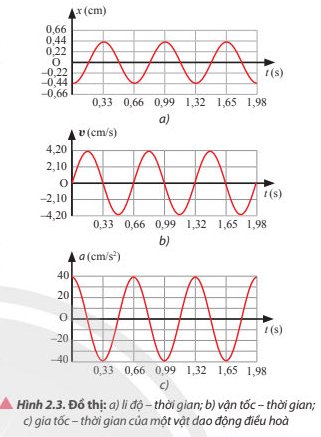
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)

Phương trình: \(x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
a)Biên độ: \(A=2cm\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
Chiều dài quỹ đạo: \(L=2A=2\cdot2=4cm\)
b)Phương trình chất điểm:
Vận tốc: \(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)\)
Gia tốc: \(a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
c)Em thay giá trị \(t=0,2s\) vào từng pt nhé.

a)Chu kì: \(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,2}{200}}=0,2s\Rightarrow\omega=\dfrac{2\pi}{T}=10\pi\)
Vật qua vị trí \(x=1,5=\dfrac{A}{2}\) theo chiều dương nên \(\varphi=-\dfrac{\pi}{3}\).
PT dao động của vật: \(x=Acos\left(\omega t+\varphi\right)=3cos\left(10\pi-\dfrac{\pi}{3}\right)\left(cm\right)\)
b)Tại \(t=1s\) thì:
Vận tốc vật:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi\cdot3\cdot sin\left(10\pi t-\dfrac{\pi}{3}\right)=-30\pi sin\left(10\pi t-\dfrac{\pi}{3}\right)\)
\(\Rightarrow v=-30\pi sin\left(10\pi\cdot1-\dfrac{\pi}{3}\right)\approx81,62cm/s\)
Gia tốc vật:
\(a=-\omega^2Acos\left(\omega t+\varphi\right)=-3000cos\left(10\pi t-\dfrac{\pi}{3}\right)\left(cm/s^2\right)\)
\(\Rightarrow a=-3000cos\left(10\pi\cdot1-\dfrac{\pi}{3}\right)=-1500\left(cm/s^2\right)\)

Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)






Phương trình vận tốc:
\(v=-4\pi\cdot5sin4\pi t=20\pi cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm/s\right)\)
Phương trình gia tốc:
\(a=-\omega^2x=-\left(4\pi\right)^2\cdot5cos4\pi t=80\pi^2cos\left(4\pi t+\pi\right)\left(cm/s^2\right)\)