Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình đã cho có 2 nghiệm trái dấu khi và chỉ khi:
\(ac< 0\Leftrightarrow-2\left(m^2-5m+4\right)< 0\)
\(\Leftrightarrow m^2-5m+4>0\Rightarrow\left[{}\begin{matrix}m>4\\m< 1\end{matrix}\right.\)

Để phương trình có nghiệm trái dấu thì \(\frac{c}{a}< 0\) hay \(ac< 0\)
\(\Leftrightarrow\left(m^2-4\right)m< 0\Leftrightarrow\orbr{\begin{cases}m^2-4>0;m< 0\\m^2-4< 0;m>0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left|m\right|>2;m< 0\\\left|m\right|< 2;m>0\end{cases}}\Leftrightarrow m< -2;0< m< 2\)
P/S Không chắc

Ta có: \(-x^2+mx+4-m^2=0\)
\(\Leftrightarrow x^2-mx+m^2-4=0\)
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=4m^2-4\left(m+2\right)\left(m-1\right)\ge0\\x_1x_2=\dfrac{m+2}{m-1}< 0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-4m+8\ge0\\-2< m< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge2\\-2< m< 1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

x 2 - ( m 3 + m - 2 ) x + m 2 + m - 5 = 0 có hai nghiệm phân biệt trái dấu khi và chỉ khi m 2 + m - 5 < 0
![]()

Phương trình bậc hai a x 2 + b x + c = 0 sẽ có hai nghiệm phân biệt trái dấu khi và chỉ khi ac < 0.
Nếu m = 1 hoặc m = -1 thì phương trỉnh đã cho có nghiệm duy nhất (loại).
( m 2 - 1 ) ( m 2 + m ) < 0 ⇔ ( m + 1 ) 2 m ( m - 1 ) < 0
⇔ 0 < m < 1

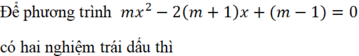


Ptr có `2` nghiệm trái dấu `<=>ac < 0`
`<=>2(m^2-4) < 0`
`<=>m^2 < 4<=>|m| < 2<=>-2 < m < 2`