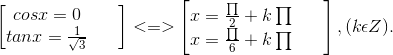Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
gợi ý: a)chia 2 vế cho căn 5
đặt \(\frac{1}{\sqrt{5}}=cosa\Rightarrow\frac{2}{\sqrt{5}}=sina\)
khi đó pt <=>sin(x-a)=\(\frac{3}{\sqrt{5}}>1\)
->vô nghiệm
bn giải thích cho mk chỗ này được ko : \(\frac{1}{\sqrt{5}}=\cos a\Rightarrow\frac{2}{\sqrt{5}}=\sin a\)
ta có \(\hept{\begin{cases}\sqrt{2}\left(sinx+cosx\right)=2sin\left(x+\frac{\pi}{4}\right)\\sinx.cosx=\frac{1}{2}sin2x=-\frac{1}{2}cos\left(2x+\frac{\pi}{2}\right)=-\frac{1-2sin^2\left(x+\frac{\pi}{3}\right)}{2}\end{cases}}\)
Vậy phương trình \(\Leftrightarrow2sin\left(x+\frac{\pi}{4}\right)+\frac{1-2sin^2\left(x+\frac{\pi}{4}\right)}{2}=1\)
Đặt \(sin\left(x+\frac{\pi}{4}\right)=a\Rightarrow PT\Leftrightarrow2a+\frac{1-2a^2}{2}=1\Leftrightarrow\orbr{\begin{cases}a=1+\frac{1}{\sqrt{2}}\\a=1-\frac{1}{\sqrt{2}}\end{cases}}\)
vì sin <1 nên \(sin\left(x+\frac{\pi}{4}\right)=1-\frac{1}{\sqrt{2}}\)có 4 nghiệm trên \(\left(0,2\pi\right)\)
\(\left\{{}\begin{matrix}\left|sinx\right|\le1\\\left|cosx\right|\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}sin^{4034}x\le sin^2x\\cos^{4038}x\le cos^2x\end{matrix}\right.\)
\(\Rightarrow sin^{4034}x+cos^{4038}x< sin^2x+cos^2x=1\) (dấu = ko xảy ra)
\(\Rightarrow\left|sin^{2017}x-cos^{2019}x\right|< \sqrt{\left(1+1\right)\left(sin^2x+cos^2x\right)}=\sqrt{2}\)
\(\Rightarrow sin^{2017}x-cos^{2019}x+\sqrt{2}>0\) \(\forall x\)
Vậy để hàm số xác định với mọi x trên đoạn đã cho
\(\Rightarrow m-sinx-cosx-2sinx.cosx\ge0\) \(\forall x\)
\(\Leftrightarrow sinx+cosx+2sinx.cosx\le m\)
Đặt \(sinx+cosx=t\Rightarrow2sinx.cosx=t^2-1\) \(\left(-1\le t\le\sqrt{2}\right)\)
\(\Rightarrow t^2+t-1\le m\Rightarrow m\ge\max\limits_{\left[-1;\sqrt{2}\right]}\left(t^2+t-1\right)=\sqrt{2}+1\)
Vậy \(m\ge\sqrt{2}+1\)
Sử dụng Bunhiacopxki thôi:
\(\left(sin^{2017}x-cos^{2019}x\right)^2\le\left(1+1\right)\left(sin^{4034}x+cos^{4038}x\right)< 2\left(sin^2x+cos^2x\right)=2\)
\(\Rightarrow-\sqrt{2}< sin^{2017}x-cos^{2019}x< \sqrt{2}\)
BĐT bên trái chuyển vế cho ta: \(sin^{2017}x-cos^{2019}x+\sqrt{2}>0\)
\(2cos^3x-sin2x.sinx=-2\sqrt{2}cos\left(x-\frac{\pi}{4}+505\pi\right)\)
\(\Leftrightarrow cos^3x-sin^2x.cosx=\sqrt{2}cos\left(x-\frac{\pi}{4}\right)\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x\right)=sinx+cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(cos^2x-sinx.cosx\right)=sinx+cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-cos^2x+sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+sinx.cosx\right)=0\)
\(\Leftrightarrow sinx\left(sinx+cosx\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\\sinx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=k\pi\end{matrix}\right.\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; 
}.
Vậy 
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ 
⇔ x = 
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; 
= (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
sin2x + 2sinxcosx - 
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ 
⇔ x = + kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 
