K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
4
H
30 tháng 6 2017
Giải:
Có:
\(S=\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)+4^3\)
Ta nhân thấy rằng trong tích \(\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)\) có một thừa số bằng 0, đó là thừa số \(2018-2018\)
Mà trong một tích, nếu có một thừa số bằng 0 thì tích đó bằng 0
\(\Leftrightarrow\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)=0\)
\(\Leftrightarrow S=\left(2018-1\right)\left(2018-2\right)...\left(2018-2018\right)+4^3=0+4^3=4^3=64\)
Vậy \(S=64\)
Chúc bạn học tốt!
AT
30 tháng 6 2017
S= (2018-1)(2018-2) .... (2018-2017) . 0 +43
=> S= 0 + 43 (Trong 1 tích có 1 thừa số bằng 0 thì tích đó bằng 0);
=>S= 4.4.4=64;
Vậy S=64
4 tháng 2 2017
2-->8: 4CS
10-->98: 45.2=90CS
100-->998: 450.3=1350CS
1000--> ?: ?.4=?CS
Số cuối cùng của dãy là:
{[(2016-4-90-1350):4]-1}.2+1000=1284
=>CS thứ 2016 của dãy là 4
7 tháng 11 2017
\(\left(3n\right)^{100}\\ =3^{100}.n^{100}\\ =\left(3^4\right)^{25}.n^{100}\\ =81^{25}.n^{100}⋮81\)
Vậy \(\left(3n\right)^{100}⋮81\)
Chúc em học tốt!
J
3
2 tháng 4 2017
Gọi \(3\) số tự nhiên liên tiếp là : \(a\)\(;\) \(a+1\)\(;\) \(a+2\) \(\left(a\in N\right)\)
Khi chia \(a\) cho \(3\) ta có các trường hợp :
\(TH1:\) \(a=3k\left(k\in N\right)\Rightarrow a⋮3\) \(\rightarrowđpcm\)
\(TH2:\) \(a=3k+1\left(k\in N\right)\Rightarrow a+2=3k+3⋮3\) \(\rightarrowđpcm\)
\(TH2:a=3k+2\left(k\in N\right)\Rightarrow a+1=3k+3⋮3\) \(\rightarrowđpcm\)
Vậy trong \(3\) số tự nhiên liên tiếp luôn có \(1\) số chia hết cho \(3\)
\(\rightarrowđpcm\)
~ Chúc bn học tốt ~
2 tháng 4 2017
Gọi 3 số tự nhiên liên tiếp lần lượt là a, a+1, a+2 (a \(\in\) N )
Xét 3 trường hợp :
+ a = 3k ( k \(\in\) N )
=> a \(⋮\) 3
+ a = 3k + 1
=> a+2 = 3k + 1 + 2
= 3k + ( 1 + 2 )
= 3k + 3
= 3(k+1) chia hết cho 3
=> (a+2) \(⋮\) 3
+ a = 3k + 2
=> a+1 = 3k + 2 + 1
= 3k + ( 2 + 1 )
= 3k + 3
= 3(k+1) chia hết cho 3
=> (a+1) \(⋮\) 3
Vậy trong ba số tự nhiên liên tiếp luôn có 1 số chia hết cho 3
T
9 tháng 4 2022
Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)
11 tháng 7 2017
Nếu là z+x thì mik biết làm nè:
Đặt x-y=2011(1)
y-z=-2012(2)
z+x=2013(3)
Cộng (1);(2);(3) lại với nhau ta được :
2x=2012=>x=1006
Từ (1) => y=-1005
Từ (3) => z=1007
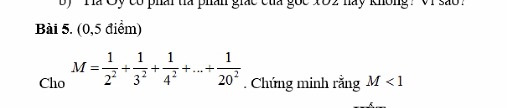
Lời giải:
Ta thấy:
$\frac{1}{2^2}< \frac{1}{1.2}$
$\frac{1}{3^2}< \frac{1}{2.3}$
$\frac{1}{4^2}< \frac{1}{3.4}$
$........$
$\frac{1}{20^2}< \frac{1}{19.20}$
Cộng lại:
$M< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{19.20}$
$M< \frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+....+\frac{20-19}{19.20}$
$M< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{19}-\frac{1}{20}$
$M< 1-\frac{1}{20}< 1$