K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2021
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\sqrt{\dfrac{2}{3}}\)
\(cos\left(a+\dfrac{\pi}{3}\right)=cosa.cos\left(\dfrac{\pi}{3}\right)-sina.sin\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{6}-3}{6}\)
20.
Đề bài sai, do \(\dfrac{3\pi}{2}>\pi\) nên không thể tồn tại góc a sao cho \(\dfrac{3\pi}{2}< a< \pi\) được
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Câu 30:
Để pt đã cho có nghiệm thì:
$\Delta=(2m+5)^2-4(m+\frac{25}{4})\geq 0$
$\Leftrightarrow 4m^2+16m\geq 0$
$\Leftrightarrow m(m+4)\geq 0$
$\Leftrightarrow m\geq 0$ hoặc $m\leq -4$
Đáp án A.
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Câu 31:
Đường trong $(C)$ có tâm $A(1,-5)$ và bán kính $R=\sqrt{45}$
Vì ĐT cần tìm song song với $x+2y+5=0$ nên nó có dạng $(I):x+2y+m=0$
$(I)$ là tiếp tuyến của $(C)$ nên:
\(d(A,(I))=R\Leftrightarrow \frac{|1-2.5+m|}{\sqrt{1^2+2^2}}=\sqrt{45}\)
$\Rightarrow m=24$ hoặc $m=-6$
Đáp án C.
8 tháng 5 2021
Câu 30 :
- Gọi PT tiếp tuyến là denta .
- Ta có denta vuông góc với d
=> PTTQ denta có dạng : \(3x+2y+c=0\)
- Xét đường tròn ( C ) có : \(\left\{{}\begin{matrix}I\left(-2;1\right)\\R=\sqrt{13}\end{matrix}\right.\)
Mà PT denta là tiếp tuyến của (C)
\(\Rightarrow R=d_{\left(denta/I\right)}=\sqrt{13}=\dfrac{\left|3.\left(-2\right)+2.1+c\right|}{\sqrt{13}}\)
\(\Rightarrow\left|c-4\right|=13\)
\(\Rightarrow\left[{}\begin{matrix}c-4=13\\c-4=-13\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=17\\c=-9\end{matrix}\right.\)
Vậy .... Đáp án C .
CM
19 tháng 2 2017
a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
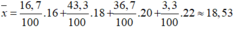
Số trung bình cộng của bảng 8 là:
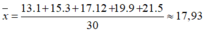
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
Ở đây chỉ thấy các câu 26, 32, 34, 36
26.
\(S_{ABC}=\dfrac{1}{2}AB^2=\dfrac{a^2}{18}\)
\(BC=AB\sqrt{2}=\dfrac{a\sqrt{2}}{3}\Rightarrow p=\dfrac{AB+AC+BC}{2}=\dfrac{2a+a\sqrt{2}}{6}\)
\(\Rightarrow r=\dfrac{S}{p}=\dfrac{6a^2}{18a\left(2+\sqrt{2}\right)}=\dfrac{\left(2-\sqrt{2}\right)a}{6}\)
32.
Đường thẳng nhận \(\overrightarrow{n}=\left(5;-1\right)\) là 1 vtpt
34.
Áp dụng định lý hàm cos:
\(c=\sqrt{a^2+b^2-2ab.cosC}=\sqrt{8^2+7^2-2.8.7.cos60^0}=\sqrt{57}\)
36.
\(y=\sqrt{\dfrac{x^2-2mx+5m}{2021}}\)
Hàm xác định trên R khi và chỉ khi: \(x^2-2mx+5m\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-5m\le0\Rightarrow0\le m\le5\)
Có 5 giá trị nguyên dương của m thỏa mãn (1;2;3;4;5)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
18.
\(-x^2+2x-5\le0\) có \(\left\{{}\begin{matrix}a=-1< 0\\\Delta'=1-5=-4< 0\end{matrix}\right.\)
\(\Rightarrow-x^2+2x-5\le0\) ; \(\forall x\in R\)
19.
Thay tọa độ lần lượt các đáp án lên thì chỉ D đúng
20.
Chu vi đường tròn: \(2\pi R=40\pi\left(cm\right)\)
Số đo của cung: \(\dfrac{35.2\pi}{40\pi}=\dfrac{7}{4}\)
TD
1
30 tháng 6 2023
8:
\(=\dfrac{cos10-\sqrt{3}\cdot sin10}{sin10\cdot cos10}=\dfrac{2\left(\dfrac{1}{2}\cdot cos10-\dfrac{\sqrt{3}}{2}\cdot sin10\right)}{sin20}=\dfrac{sin\left(30-10\right)}{sin20}=1\)
10:
\(=\left(2-\sqrt{3}\right)^2+\left(2+\sqrt{3}\right)^2\)
=7-4căn 3+7+4căn 3=14
12:
\(=cos^270^0+\dfrac{1}{2}\left[cos60-cos140\right]\)
\(=cos^270^0+\dfrac{1}{2}\cdot\dfrac{1}{2}-\dfrac{1}{2}\cdot2cos^270^0+\dfrac{1}{.2}\)
=1/4+1/2=3/4
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
10.
\(\dfrac{sin3x-cos3x}{sinx+cosx}=\dfrac{3sinx-4sin^3x-\left(4cos^3x-3cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(1-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{\left(sinx+cosx\right)\left(3-4+4sinx.cosx\right)}{sinx+cosx}\)
\(=-1+4sinx.cosx\)
\(=2sin2x-1\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
11.
\(tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{1+cos\left(\dfrac{\pi}{2}+x\right)}{sin\left(\dfrac{\pi}{2}+x\right)}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1+sin\left(-x\right)}{cos\left(-x\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1-sinx}{cosx}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}-2sin\dfrac{x}{2}cos\dfrac{x}{2}}{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)^2}{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)\left(cos\dfrac{x}{2}+sin\dfrac{x}{2}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\dfrac{x}{2}-sin\dfrac{x}{2}}{cos\dfrac{x}{2}+sin\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}{sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).cot\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\)
\(=1\)
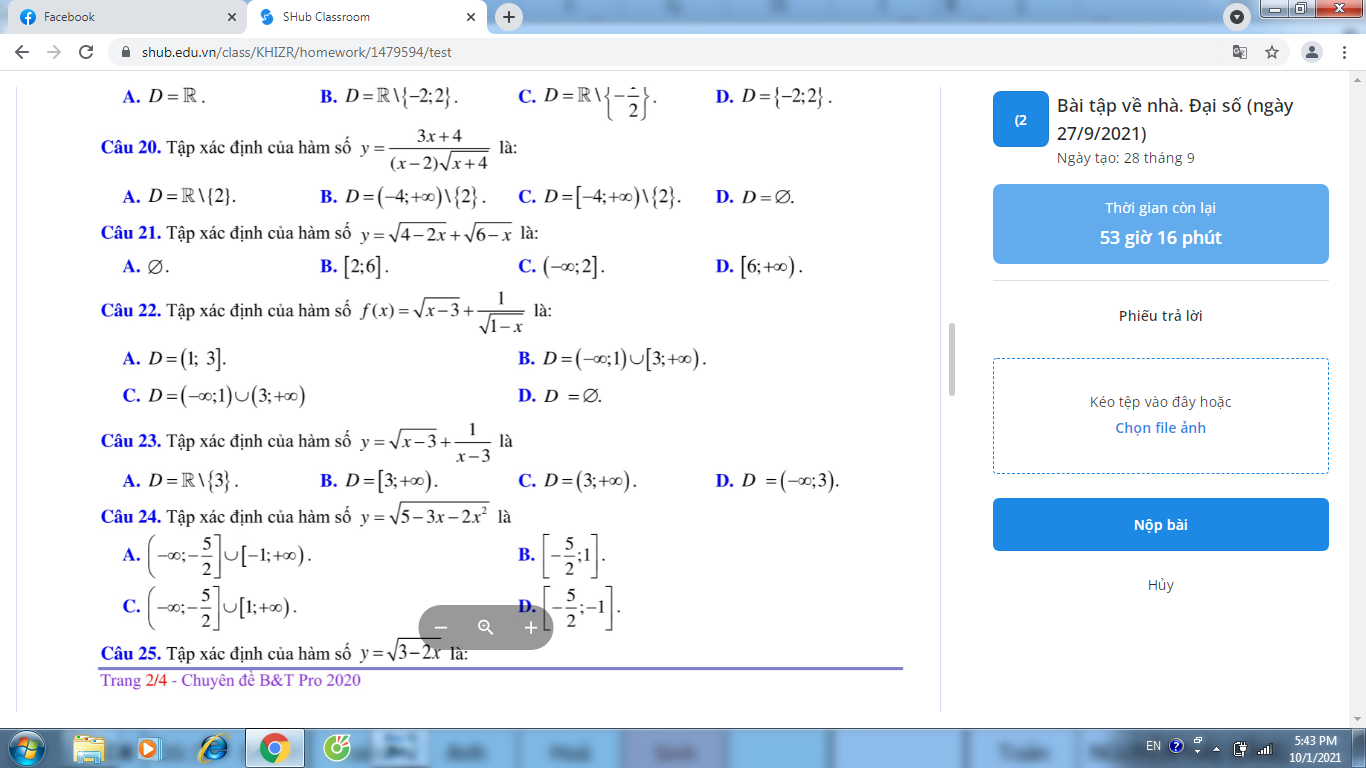
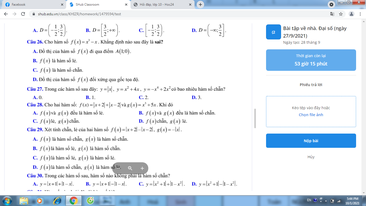
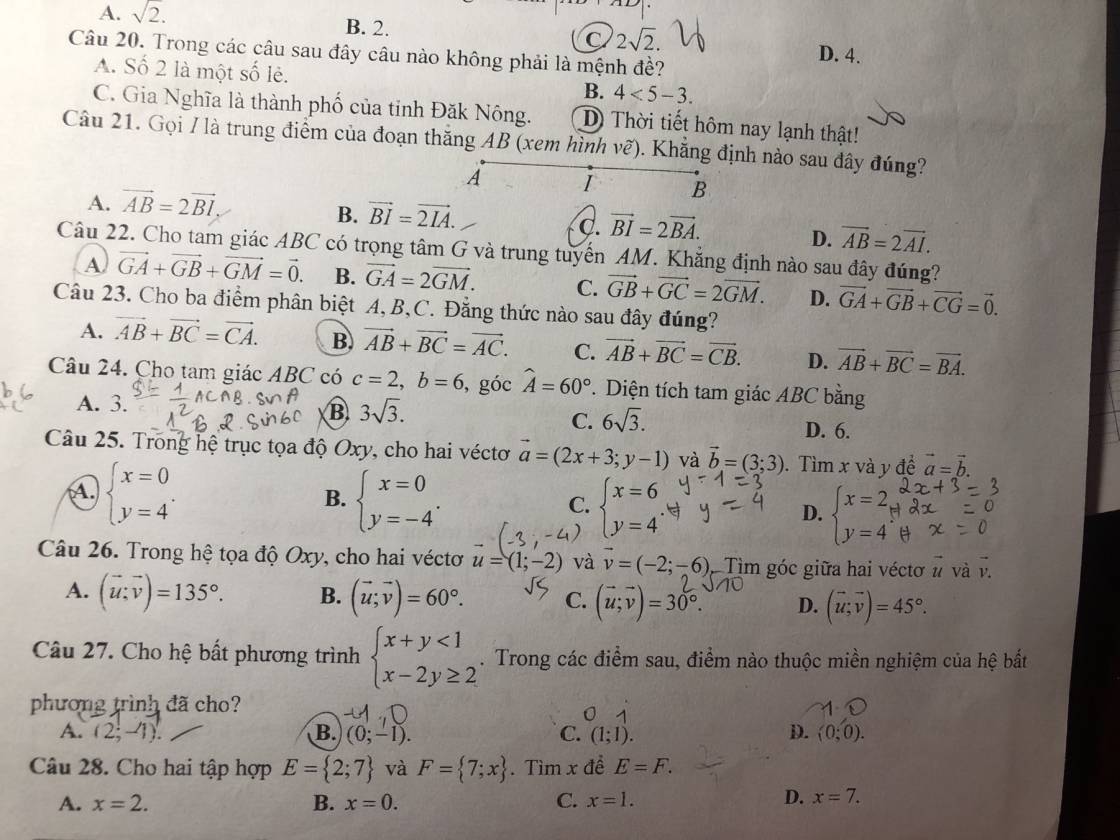
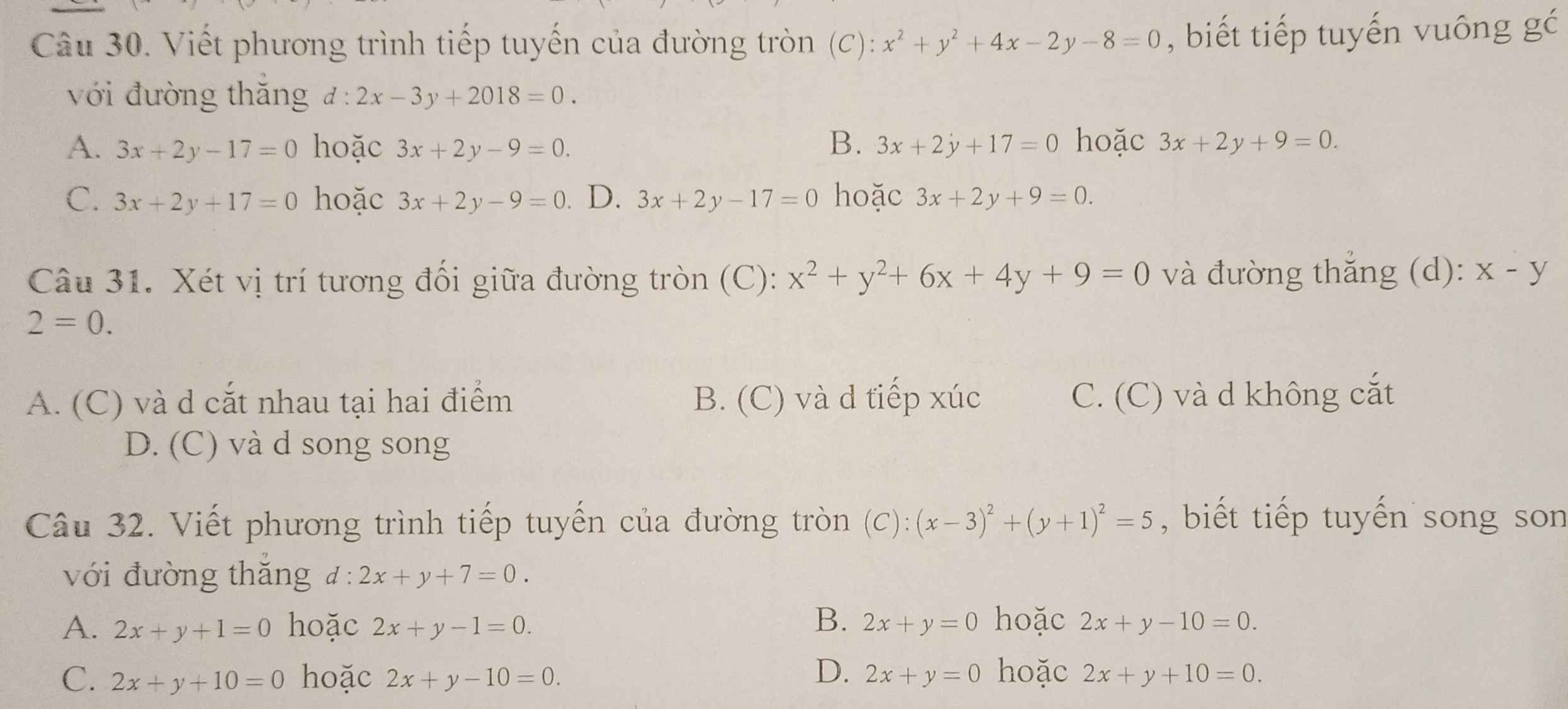
câu 20 đến 25 đc r ạ