Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì hình trụ và hình nón có cùng chiều cao nên:
Thể tích hình trụ : V 1 = πr 2 h
Thể tích hình nón : V 2 = (1/3). πr 2 .h
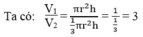
Vậy chọn đáp án C

Thể tích của hình trụ là: π m 2 k
Thể tích của hình nón là: 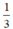 π
m
2
k
π
m
2
k
Vậy thể tích của hình nón bằng 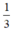 thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là
thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là 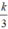

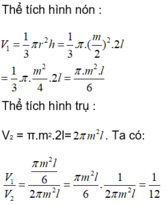
Vậy khi múc đầy nước vào hình nón và đổ vào hình trụ (Không chứa gì cả) thì độ cao của nước trong hình trụ là 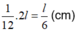
Vậy chọn đáp án A
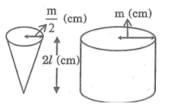
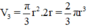
Bạn kiểm tra lại đề bài? S max thì S là diện tích xung quanh hay diện tích toàn phần ạ. Hay là V max vậy?
Mình làm S xung quanh max nhé!
Không vẽ được hình. Bạn thông cảm:
+) Gọi chiều cao của hình trụ là: h' ; bán kính đáy là r'
Áp dụng định lí ta - let ta có: \(\frac{h'}{h}=\frac{r-r'}{r}=1-\frac{r'}{r}\)
<=> \(\frac{h'}{18}=1-\frac{r'}{9}\)
<=> \(h'=18-2r'\)
Công thức tính xung quanh của hình trụ:
\(S_{xq}=2\pi r'h'=2\pi r'\left(18-2r'\right)=-4.\pi r'^2+36.\pi r'\)
\(=-4\pi\left(r'^2-9r+\frac{81}{4}\right)+81\pi\)
\(=-4\pi\left(r'-\frac{9}{2}\right)^2+81\pi\le81\pi\)
=> S toàn phần max = 81 pi
khi đó: r' = 9/2 và h' = 9
em xin lỗi chị đấy là V ạ=))