Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi sự kiện A là vị trí này có nước ngầm, sự kiện B là máy báo đúng.
Ta có:
P(A) = 7/10 (vì cứ 10 địa điểm bị nghi vấn thì có 7 vị trí là có nước ngầm)
P(B|A) = 0.85 (vị trí có nước ngầm máy báo đúng với xác suất 0.85)
P(~B|~A) = 0.9 (vị trí không có nước ngầm máy báo sai với xác suất 0.1)
`(a)` Ta cần tính xác suất P(A|B), tức là vị trí này có nước ngầm khi máy báo đúng.
Theo công thức Bayes, ta có:
P(A|B) = P(B|A) * P(A) / P(B)
Trong đó:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) (theo định lý xác suất toàn phần)
P(~A) = 1 - P(A) (vì chỉ có hai khả năng: có nước ngầm hoặc không có nước ngầm)
Thay giá trị vào ta được:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) = 0.85 * 7/10 + 0.9 * 3/10 = 0.865
P(A|B) = P(B|A) * P(A) / P(B) = 0.85 * 7/10 / 0.865 ≈ 0.692
Vậy xác suất vị trí này có nước ngầm khi máy báo đúng là khoảng 69.2%.
`(b)` Ta cần tính xác suất P(B), tức là máy báo đúng.
Theo công thức Bayes, ta có:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A)
Thay giá trị vào ta được:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) = 0.85 * 7/10 + 0.1 * 3/10 = 0.655
Vậy xác suất máy báo đúng là khoảng 65.5%.


Đây là công thức bạn phải thuộc lòng, còn b là số lớn 0 và khác 1, tùy vào bài tập bạn giải sẽ có số b hợp lý.
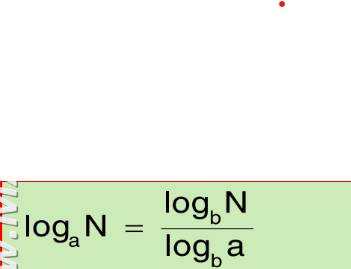
khum bn