Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



=A=\(\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}+\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\)
có (a+b)3=a3+3a2b+3ab2+b3
=a3+b3+3ab(a+b)
Ad ta có
A3=2+3(\(\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}+\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\)) .
(\(\sqrt[3]{\left(1+\dfrac{\sqrt{84}}{9}\right)\left(1-\dfrac{\sqrt{84}}{9}\right)}\))
A3=2+3A\(\sqrt[3]{1-\dfrac{84}{81}}\)
A3=2-A
=>A3+A-2=0
=>A3-A+2A-2=0
=>A(A2-1)+2(A-1)=0
=>A(A-1)(A+1)+2(A-1)=0
=>(A-1)(A2+A+2)=0
=>(A-1)(A2+2.\(\dfrac{1}{2}\)A+\(\dfrac{1}{4}\)+\(\dfrac{7}{4}\))=0
=>(A-1)((A+\(\dfrac{1}{2}\))2+\(\dfrac{7}{4}\))=0
=> A=1
hoặc (A+\(\dfrac{1}{2}\))2+\(\dfrac{7}{4}\)=0(loại)
vậy A nguyên

Đặt \(A=\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}+\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\)
\(\Rightarrow A^3=1+\dfrac{\sqrt{84}}{9}+1-\dfrac{\sqrt{84}}{9}+3A.\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}.\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\)
\(\Leftrightarrow A^3=2+3A.\sqrt[3]{1-\dfrac{84}{81}}\)
\(\Leftrightarrow A^3=2+3A.\sqrt[3]{-\dfrac{3}{81}}=2+3A.\sqrt[3]{-\dfrac{1}{27}}\)
\(\Leftrightarrow A^3=2-A\)
\(\Leftrightarrow A^3+A-2=0\)
\(\Leftrightarrow\left(A-1\right)\left(A^2+A+2\right)=0\)
Dể thấy \(A^2+A+2=\left(A+\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
\(\Rightarrow A-1=0\Leftrightarrow A=1\)
Vậy \(\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}+\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\) là số nguyên (đpcm)

a) \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
= \(2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}\)
= \(-\sqrt{5}+15\sqrt{2}\)
b) \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)
= \(\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)
= \(2.7-2\sqrt{21}+7+2\sqrt{21}=14+7=21\)
c) \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)
= \(6+2\sqrt{6}.\sqrt{5}+5-2\sqrt{30}\)
= \(11+2\sqrt{30}-2\sqrt{30}=11\)
d) \(\left(\dfrac{1}{2}-\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}\)
= \(\left(\dfrac{1}{2}-\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+8\sqrt{2}\right).8\)
= \(4-4\sqrt{2}-12\sqrt{2}+64\sqrt{2}=4+48\sqrt{2}\)
Bài này dễ ẹc ( đâu có khó đâu :)) )
a) \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
\(=\sqrt{2^2.5}-\sqrt{3^2.5}+3\sqrt{3^2.2}+\sqrt{6^2.2}\)
\(=2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}\)
\(=\left(2-3\right)\sqrt{5}+\left(9+6\right)\sqrt{2}\)
\(=15\sqrt{2}-\sqrt{5}\)
b) \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)
\(=\sqrt{2^2.7}.\sqrt{7}-2\sqrt{3}.\sqrt{7}+\sqrt{7}.\sqrt{7}+\sqrt{2^2.21}\)
\(=2.7-2\sqrt{21}+7+2\sqrt{21}\)
\(=14+7+\left(2-2\right)\sqrt{21}=21\)
c) \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)
\(=6+2\sqrt{30}+5-\sqrt{2^2.30}\)
\(=6+5+2\sqrt{30}-2\sqrt{30}=11\)
d) \(\left(\dfrac{1}{2}\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}\)
\(=\left(\dfrac{1}{2}\sqrt{\dfrac{2}{2^2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{10^2.2}\right):\dfrac{1}{8}\)
\(=\left(\dfrac{1}{4}\sqrt{2}-\dfrac{3}{2}\sqrt{2}+8\sqrt{2}\right).8\)
\(=2\sqrt{2}-12\sqrt{2}+64\sqrt{2}=54\sqrt{2}\)
Hok tốt

a, \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)
= \(2\sqrt{3}-10\sqrt{3}-\dfrac{\sqrt{3}\cdot\sqrt{11}}{\sqrt{11}}+5\sqrt{\dfrac{4}{3}}\)
= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+5\sqrt{\dfrac{12}{3^2}}\)
= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+5\dfrac{2\sqrt{3}}{3}\)
= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)
= \(-9\sqrt{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{-27\sqrt{3}}{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{-17\sqrt{3}}{3}\)
b, \(\sqrt{150}+\sqrt{1,6}\cdot\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
= \(5\sqrt{6}+\dfrac{2\sqrt{10}}{5}\cdot2\sqrt{15}+4,5\sqrt{\dfrac{8}{3}}-\sqrt{6}\)
= \(5\sqrt{6}+4\sqrt{6}+4,5\sqrt{\dfrac{24}{3^2}}-\sqrt{6}\)
= \(5\sqrt{6}+4\sqrt{6}+4,5\cdot\dfrac{2\sqrt{6}}{3}-\sqrt{6}\)
= \(5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}=11\sqrt{6}\)
c, \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\)
= \(\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\)
= \(\left(3\sqrt{7}-2\sqrt{3}\right)\cdot\sqrt{7}+2\sqrt{21}\)
= \(21-2\sqrt{21}+2\sqrt{21}=21\)
d, \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)
= \(6+2\sqrt{30}+5-2\sqrt{30}=11\)

bài 1:
a: Ta có: \(2\sqrt{18}-9\sqrt{50}+3\sqrt{8}\)
\(=6\sqrt{2}-45\sqrt{2}+6\sqrt{2}\)
\(=-33\sqrt{2}\)
b: Ta có: \(\left(\sqrt{7}-\sqrt{3}\right)^2+7\sqrt{84}\)
\(=10-2\sqrt{21}+14\sqrt{21}\)
\(=12\sqrt{21}+10\)
Bài 2:
a: Ta có: \(\sqrt{\left(2x+3\right)^2}=8\)
\(\Leftrightarrow\left|2x+3\right|=8\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=8\\2x+3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{11}{2}\end{matrix}\right.\)
b: Ta có: \(\sqrt{9x}-7\sqrt{x}=8-6\sqrt{x}\)
\(\Leftrightarrow4\sqrt{x}=8\)
hay x=4
c: Ta có: \(\sqrt{9x-9}+1=13\)
\(\Leftrightarrow3\sqrt{x-1}=12\)
\(\Leftrightarrow x-1=16\)
hay x=17
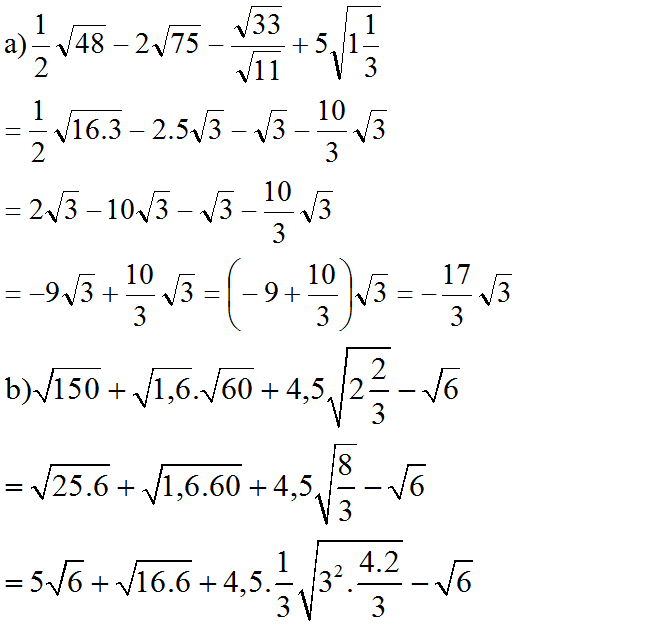
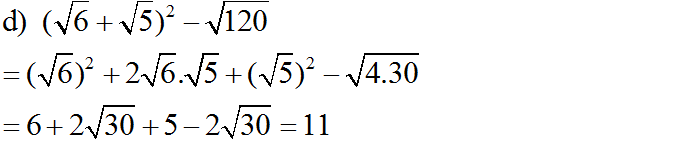
Lời giải:
Đặt \(\sqrt[3]{1+\frac{\sqrt{84}}{9}}=a; \sqrt[3]{1-\frac{\sqrt{84}}{9}}=b\)
Khi đó:
\(a^3+b^3=1+\frac{\sqrt{84}}{9}+1-\frac{\sqrt{84}}{9}=2\)
\(ab=\sqrt[3]{\left(1+\frac{\sqrt{84}}{9}\right)\left(1-\frac{\sqrt{84}}{9}\right)}=\sqrt[3]{1-\frac{84}{81}}=\frac{-1}{3}\)
Suy ra:
\(D^3=(a+b)^3=a^3+b^3+3ab(a+b)=2+3.\frac{-1}{3}.D\)
\(\Leftrightarrow D^3=2-D\Leftrightarrow D^3+D-2=0\)
\(\Leftrightarrow D^2(D-1)+D(D-1)+2(D-1)=0\)
\(\Leftrightarrow (D-1)(D^2+D+2)=0\)
Dễ thấy \(D^2+D+2>0\Rightarrow D-1=0\Leftrightarrow D=1\)
Vậy $D$ là một số nguyên.