Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều rộng là x
=>Chiều dài là 3x
Theo đề, ta có: (x+5)(3x+5)=135
=>3x^2+5x+15x+25-135=0
=>3x^2+20x-110=0
=>\(x=\dfrac{-10+\sqrt{430}}{3}\)
=>Chiều dài ban đầu là (-10+căn 430)(cm)
Chu vi ban đầu là:
\(\left(-10+\sqrt{430}-\dfrac{10}{3}+\dfrac{1}{3}\cdot\sqrt{430}\right)\cdot2\)
\(=\left(-\dfrac{40}{3}+\dfrac{4}{3}\cdot\sqrt{430}\right)\cdot2\)
\(=\dfrac{-20}{3}+\dfrac{2}{3}\cdot\sqrt{430}\left(cm\right)\)

`a, = (a+5)(a+5)5 - 125 = 5(a+5)^2 - 125 = 5a^2 + 50a.`
`b, = (a+5)^3 - 125 = a^3 + 15a^2 + 75a`
Thể tích hình hộp chữ nhật ban đầu là \(5 \times 5 \times 5 = 125\) cm³.
a/ Khi chiều dài và chiều rộng tăng thêm \(a\) cm, thể tích mới sẽ là \((5+a) \times (5+a) \times 5 = 25a + 10a² + 125\).
Thể tích tăng thêm \(25a + 10a²\).
b/ Khi cả ba chiều tăng thêm \(a\) cm, thể tích mới sẽ là \((5+a) \times (5+a) \times (5+a) = 125 + 75a + 15a² + a³\).
Thể tích tăng thêm \(75a + 15a² + a³\)

Gọi chiều rộng ban đầu là x(cm)(Điều kiện: x>0)
Chiều dài ban đầu là: 2x(cm)
Vì khi chiều rộng tăng 2cm thì diện tích tăng 4cm2 nên ta có phương trình:
\(2x\cdot\left(x+2\right)=2x^2+4\)
\(\Leftrightarrow2x^2+4x-2x^2-4=0\)
\(\Leftrightarrow4x=4\)
hay x=1(thỏa ĐK)
Chiều dài ban đầu là: \(2\cdot1=2\left(cm\right)\)
Vậy: Chiều rộng ban đầu là 1cm
Chiều dài ban đầu là 2cm

Gọi chiều dài HCN là 3a và chiều rộng HCN là a (a > 0)
Theo bài ra, ta có: \(\left(3a+5\right)\left(a+5\right)=180\)
\(\Leftrightarrow3a^2+20a+25=153\)
\(\Leftrightarrow3a+20a+25-153=153-153\)
\(\Leftrightarrow3a^2+20a-128=0\)
\(\Leftrightarrow3a^2+32a-12a-128=0\)
\(\Leftrightarrow a\left(3a+32\right)-4\left(3a+32\right)=0\)
\(\Leftrightarrow\left(a-4\right)\left(3a+32\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=4\left(t/m\right)\\a=-\frac{32}{3}\left(loai\right)\end{cases}}\)
\(a=4\Rightarrow3a=12\) (thỏa mãn)
Vậy hình chữ nhật đó có chiều dài 12 cm và chiều rộng 4 cm.
Chúc bạn học tốt.

Gọi chiều rộng là x(cm) x>0
Chiều dài là :\(\dfrac{5}{4}\) x(cm)
Theo bài ra ta có pt :
\(\dfrac{5}{4}\)x+3=x+8
Giải ra được x=20
Chiều dài là : \(\dfrac{5}{4}\) .20=25
Diện tích của hcn là : 20.25=500(cm\(^2\) )

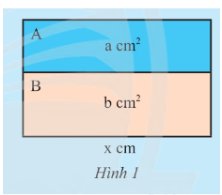
a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)
Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)
Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)
Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)
b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)

a) Chiều dài, chiều cao hình hộp chữ nhật \(A\) là: \(2xk\)
Diện tích đáy của hình hộp chữ nhật \(A\) là: \(2xk.2x = 4k{x^4}\)
b) Thể tích của hình hộp chữ nhật \(A\) là: \(2xk.2x.2xk = 8{k^2}{x^3}\)

Chiều dài của A:
2kx
Chiều cao của A:
2kx
a) Diện tích đáy của A:
2x . 2kx = 4kx²
b) Thể tích của A:
V = 4kx² . 2kx = 8k²x³

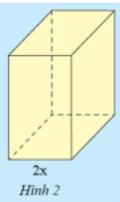

Diện tích hình A: ` 2x . 2kx = 4x^2k (cm^2)`
Chiều rộng hình B: `4x^2k : 3x = 4/3xk (cm)`.