Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N P Q
Dễ dàng thấy ngay rằng các đoạn QM, PN, QP, MN là đường trung bình của các tam giác ADB, CDB, ADC, ABC.
Vậy thì QM song song và bằng PN hay tứ giác MNPQ là hình bình hành.
+) Để hình bình hành MNPQ là hình bình chữ nhật thì \(QM\perp MN\Leftrightarrow AC\perp BD\Leftrightarrow\) Hình bình hành ABCD là hình thoi.
+) Để hình bình hành MNPQ là hình bình thoi thì QM = MN hay AC = BD \(\Leftrightarrow\) Hình bình hành ABCD là hình chữ nhật.
+) Để hình bình hành MNPQ là hình vuông thì nó phải là hình chữ nhật và hình thoi, hay hình bình hành ABCD cũng là hình chữ nhật và hình thoi. Nói cách khác, ABCD phải là hình vuông.

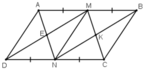
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC; 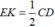 (vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
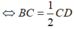
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành