Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức  là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức 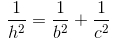
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.

Hình bạn tự vẽ nha.
a, ABCD là hình vuông \(\Rightarrow AB=BC=CD=AD\)
Ta có: \(\hat{IAD}+\hat{DAE}=90^o\)
\(\hat{BAE}+\hat{DAE}=90^o\)
\(\Rightarrow \hat{IAD} =\hat{BAE}\)
Xét \(\Delta ADI\) và \(\Delta ABE\) có:
\(\hat{ADI}=\hat{ABE}=90^o\)
\(AD=AB\left(cmt\right)\)
\(\hat{IAD}=\hat{BAE}(cmt)\)
\(\Rightarrow\Delta ADI=\Delta ABE\left(g-c-g\right)\Rightarrow AI=AE\)
b, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow AD.IK=AI.AK\) (hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow AD.IK=AE.AK\)
c, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AI^2}+\dfrac{1}{AK^2}\)(hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) mà hình vuông ABCD không đổi \(\Rightarrow\) AD không đổi\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi
Vậy \(\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi khi E thay đổi trên cạnh BC
Hai câu cuối í ẹ chưa nghĩ ra, để sau.

a: Xét ΔABC vuông tại A có cos B=AB/BC
=>AB/BC=1/2
=>AB=3cm
=>AC=3 căn 3(cm)
b: \(HB=\dfrac{AB^2}{BC}=1.5\left(cm\right)\)
HC=6-1,5=4,5(cm)

Câu 1:
a: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot CB}{CH\cdot CB}=\dfrac{BH}{CH}\)
b: \(BD\cdot CE\cdot BC\)
\(=\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\cdot BC\)
\(=AH^4\cdot\dfrac{BC}{AB\cdot AC}=\dfrac{AH^4}{AH}=AH^3\)

a)Có :\(\widehat{EBD}=\widehat{BAD}\)(cùng chắn \(\stackrel\frown{BD}\))
\(\widehat{BED}\):chung
\(\Rightarrow\Delta EBD\sim\Delta EAB\left(gg\right)\)
\(\Rightarrow\dfrac{BE}{ED}=\dfrac{EA}{BE}\)\(\Rightarrow EB^2=ED.EA\)(đpcm)
Xét \(\Delta EDC\) và \(\Delta EAC\), có:
\(\widehat{DEC}\):chung;
\(\widehat{ECD}=\widehat{DAC}\)(cùng chắn \(\stackrel\frown{CD}\))
\(\Rightarrow\Delta EDC\sim\Delta ECA\left(gg\right)\)
\(\Rightarrow\dfrac{ED}{EC}=\dfrac{CD}{AC}\)và EB=EC(t/c 2 tt cắt nhau)
Có \(\Delta EBD\sim\Delta EAB\)
\(\Rightarrow\dfrac{BD}{AB}=\dfrac{ED}{EB}\)
\(\Rightarrow\dfrac{CD}{AC}=\dfrac{ED}{EB}=\dfrac{BD}{AB}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
b)Có ABDC nt( \(A,B,D,C\in\left(O\right)\))(1)
Có xy//d(gt)
\(\Rightarrow\widehat{xAP}=\widehat{BPE}\)(SLT)
Có \(\widehat{ADB}=\widehat{xAP}\)(cùng chắn \(\stackrel\frown{AB}\))
\(\Rightarrow\widehat{BPE}=\widehat{ADB}\)\(\Rightarrow\)BDEP nt\(\Rightarrow B,D,E,P\)thuộc 1 đường tròn(2)
Có xy//d
\(\Rightarrow\widehat{CAy}=\widehat{CQE}\)(SLT)
Có: \(\widehat{CAy}=\widehat{ADC}\)(cùng chắn \(\stackrel\frown{AC}\))
\(\Rightarrow\widehat{CQE}=\widehat{ADC}\Rightarrow\)CDEQ nt\(\Rightarrow\)C,D,E,Q thuộc 1 đường tròn(3).
Từ (1),(2),(3)\(\Rightarrow\)Đường tròn ngoại tiếp (ABDC),(BDEP),(CDEQ) cùng đi qua D.
Mà tâm đường tròn ngoại tiếp (ABDC) cũng là tâm đường tròn ngoại tiếp (ABC).
Mà tâm đường tròn ngoại tiếp (BDEP) cũng là tâm đường tròn ngoại tiếp (BEP).
Mà tâm đường tròn ngoại tiếp (CDEQ) cũng là tâm đường tròn ngoại tiếp (CEQ).
Vậy đường tròn ngoại tiếp (ABC),(BEP).(CEQ) cùng đi qua D.
Giải gấp em câu d) ạ.
