Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

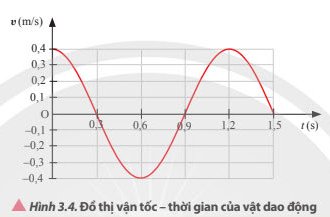
Tốc độ cực đại của vật trong quá trình dao động là 0,4 m/s
Thế năng cực đại của vật trong quá trình dao động là
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.0,4^2=0,16\left(J\right)\).

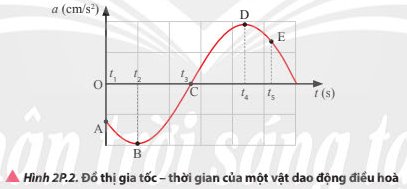
Vị trí A có gia tốc a1=−ω2.A
Vị trí B có gia tốc a2=0 nên vật ở vị trí cân bằng có vận tốc bằng v=ωA
Vị trí C có gia tốc a3=−ω2.A>0 nên vật ở vị trí biên âm có vận tốc bằng 0

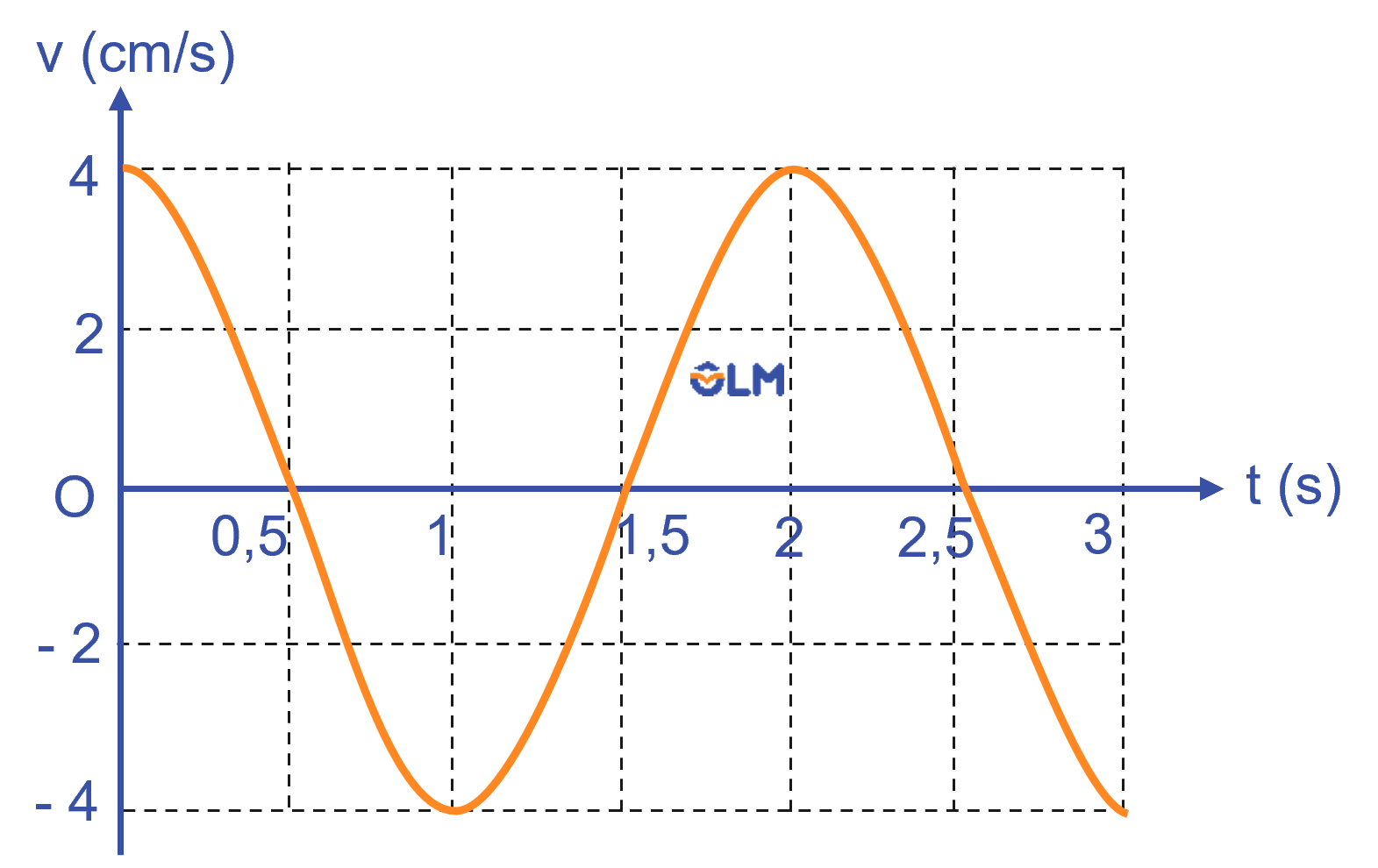
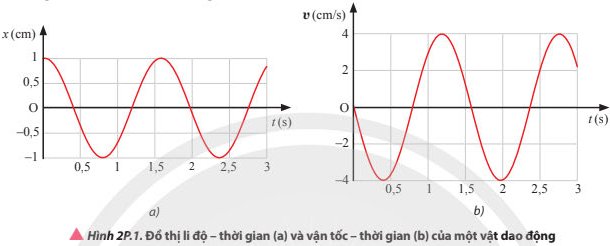
Từ đồ thị ta xác định được A = 1cm
Ta có: vmax = ωA⇒ω = 4 (rad/s)
Phương trình li độ của dao động: x = cos(4t) (cm)
Phương trình vận tốc của dao động: v = 4cos(4t+\(\frac{\pi }{2}\)) (cm/s)
Phương trình gia tốc của vật dao động: a = 16cos(4t) (m/s2)

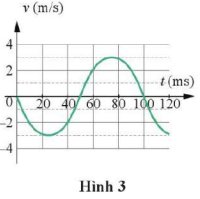
a) Chu kì T = 100 ms = 0,1 s
b) Vận tốc có độ lớn cực đại: vmax = 3 m/s
c) Tần số góc: $\omega = \frac{2 \pi}{T} =\frac{2 \pi}{0.1} = 20 \pi (rad/s)$
Biên độ của dao động: $A=\frac{v_{max}}{\omega} =\frac{3}{20 \pi} \approx 0,048m$
Cơ năng của vật dao động:
$W=W_{dmax}=\frac{1}{2}mv^{2}_{max}\frac{1}{2}.0,15.3^{2}=0,675J$
d) Tại thời điểm 100 ms vận tốc bằng 0 và đang đi theo chiều âm nên vật có vị trí tại biên dương.
Khi đó gia tốc:
$a=-\omega ^{2}A=-(20 \pi)^{2}.0,048=-19,5 m/s^{2}$

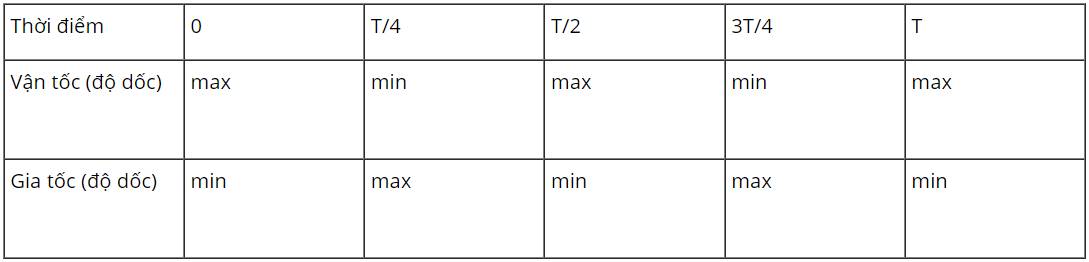
Trên đồ thị (v – t) Hình 3.2, tại thời điểm \(\dfrac{T}{4}\), \(\dfrac{3T}{4}\) độ dốc của đồ thị bằng 0 và tại thời điểm 0, \(\dfrac{T}{2}\), T độ dốc của đồ thị cực đại. Trên đồ thị (a - t) Hình 3.3 thì ngược lại.

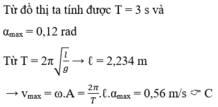


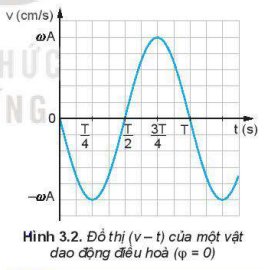
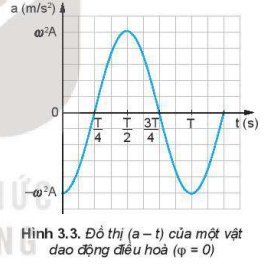
1. Vật tại vị trí cân bằng có vmax = ωA = 20 cm/s
Khi vật có tốc độ bằng v = \(\omega.\sqrt{A^2-x^2}=10\left(\dfrac{cm}{s}\right)\)
Gia tốc của vật có độ lớn a = ω2x = \(40\sqrt{3}\) cm/s2
Từ đó A = 5 cm, ω = 4rad/s
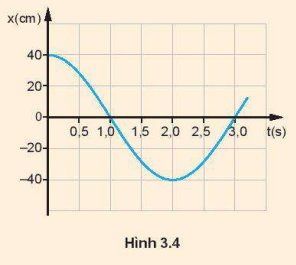
2. Từ đồ thị ta thấy:
Biên độ A = 40 cm, chu kì T = 4s
a) Tốc độ của vật ở thời điểm t = 0s bằng v = 0 (cm/s) vì ở vị trí biên.
b) Tốc độ cực đại của vật là vmax = ωA = 20π (rad/s).
c) Gia tốc của vật tại thời điểm t = 1,0 s là a= ω2A=10π2 (rad/s) đạt giá trị lớn nhất vì tại vị trí cân bằng.