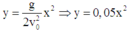Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(chọn\) \(O\) \(trùng\) \(mặt\) \(đất\)\(,chiều\left(+\right)\) \(hướng\) \(lên\)
\(a,\Rightarrow\left\{{}\begin{matrix}x=xo+vot-\dfrac{1}{2}gt^2=10+30t-5t^2\\v=vo-gt\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}0=10+30t-5t^2\\v=30-10t\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}t=3+\sqrt{11}\approx6,3\left(s\right)\left(thỏa\right)\\t=3-\sqrt{11}\approx-0,3\left(s\right)\left(loại\right)\end{matrix}\right.\\v=30-10.6,3=-33\left(m/s\right)\end{matrix}\right.\)
\(b,\Rightarrow\left\{{}\begin{matrix}0=30-10tmax\\x=hmax=10+30t-5t^2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}t\left(max\right)=3s\\x=hmax=10+30.3-5.3^2=55m\end{matrix}\right.\)
\(c,TH1:2s\rightarrow4s\Rightarrow t1< tmax< t2\)
\(\Rightarrow\Delta S=\left|hmax-x1\right|+\left|hmax-x2\right|=\left|55-\left(10+30.2-5.2^2\right)\right|+\left|55-\left(10+30.4-5.4^2\right)\right|=10m\)
\(TH2:2s\rightarrow6s\Rightarrow t1< tmax< t2\Rightarrow\Delta S=\left|hmax-x1\right|+\left|hmax-x2\right|=50m\)

Ta có:
+ Theo phương Ox: v x = v 0
+ Theo phương Oy: v y = g t
Độ lớn của vận tốc tại vị trí bất kì: v = v x 2 + v y 2 = v 0 2 + g 2 t 2
Đáp án: B

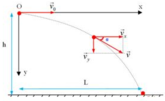
Phương trình chuyển động:
+ Theo phương Ox: x = v 0 t (1)
+ Theo phương Oy: y = 1 2 g t 2 (2)
Phương trình quỹ đạo (thay t ở (1) vào (2)): y = g 2 v 0 2 x 2
=> phương trình quỹ đạo của vật ném ngang trong trường hợp trên: y = g 2 v 0 2 x 2 = 10 2.10 2 = 0 , 05 x 2
Đáp án: C

a)
Chọn chiều (+) hướng lên. Gốc thời gian lúc bắt đầu ném
\(y=v_0t+\frac{gt2}{2}=20t-5t^2\) (1)
\(v=v_0+gt=20-10t\) (2)
Tại điểm cao nhất v=0
Từ (2) \(\Rightarrow\) t=2(s) thay vào (1)
yM = 20(m)
b)
Khi chạm đất y=0 từ (1)\(\Rightarrow\) t=0 và t=4 (s)
Thay t = 4 (s) vào (2) \(v'=-20m\text{/}s\)
(Dấu trừ (-) vận tốc ngược với chiều dương.)

Chọn hệ quy chiếu gắn với mặt đất, chiều dương hướng lên, chọn mặt đất làm vật mốc
a. Ox: v0x=v=30m/s ; ax=0
Oy: v0Y=0 ; ay=-g=-10 m/s2
Ta có: x=v0X.t=30t \(\Leftrightarrow t=\dfrac{x}{30}\)
y=\(y_0+\dfrac{1}{2}at^2\)=\(y_0-\dfrac{1}{2}gt^2\) \(=80-\dfrac{1}{2}.10.\dfrac{x^2}{30^2}\)
\(\Leftrightarrow y=80-\dfrac{1}{180}x^2\)
Có : \(y=80-\dfrac{1}{2}.10.t^2\), thay y=0 ta được: t=4 (s)
Vậy thời gian kể từ lúc ném đến lúc chạm đất là 4(s)
c. Tầm xa của vật là: L=x=v0X.t=30.4=120 (m)

Chọn mốc thế năng tại mặt đất
a) Cơ năng của vật: \(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}m.10^2+m.10.20=250m\)
Khi vật lên độ cao cực đại thì cơ năng là: \(W_2=mgh_{max}=m.10.h_{max}\)
Bảo toàn cơ năng ta có: \(W_2=W\Rightarrow h_{max}=25(m)\)
b) Khi chạm đất, cơ năng của vật là: \(W_3=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng ta có: \(W_3=W\Rightarrow \dfrac{1}{2}mv^2=250m\Rightarrow v=10\sqrt 5(m/s)\)
c) Tại vị trí Wđ= Wt \(\Rightarrow W= 2W_t=2.mgh=mgh_{max}\)
\(\Rightarrow h=\dfrac{h_{max}}{2}=12,5(m)\)
@Bình Trần Thị: \(W_đ=W_t\)
Suy ra cơ năng: \(W=W_đ+W_t=W_t+W_t=2W_t\)