Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét tam giác ACD và tam giác ECD(đều là vuông)![]()
ECD=DCA(Vì CD là p/giác)
CD là cạnh chung
\(\Rightarrow\)tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
b)Vì tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
\(\Rightarrow\)AD=DE(cạnh cặp tương ứng)
\(\Rightarrow\)D cách đều hai mút của AE
\(\Rightarrow\)CD là đường trung trực của AE
Do đó CI\(\perp\)AE
\(\Rightarrow\)Tam giác CIE là tam giác vuông
c)Vì AD=DE(câu b)
Mà tam giác BDE là tam giác vuông(tại E)
\(\Rightarrow\)DE<BD(cạnh góc vuông nhỏ hơn cạnh huyền)
\(\Rightarrow\)AD<BD(đpcm)
d)Kéo dài BK cắt AC tại O
Vì BK\(\perp\)CD(gt)
\(\Rightarrow\)CK là đường cao thứ nhất của tam giác OBC(1)
Vì tam giác ABC vuông tại A
Nên BA\(\perp\)AC
\(\Rightarrow\)BA là đường cao thứ hai của tam giác OBC(2)
Theo đề bài ta có DE\(\perp\)BC
Nên DE là đường cao thứ ba của tam giác OBC(3)
Từ (1),(2) và (3) suy ra:
Ba đường cao giao nhau tại một điểm trùng với điểm D
\(\Rightarrow\) 3 đường thẳng AC;DE;BK đồng quy(đpcm)

MQ là đường trung bình tam giác ABD \(\Rightarrow\overrightarrow{MQ}=\frac{1}{2}\overrightarrow{BD}\)
NP là đường trung bình tam giác CBD \(\Rightarrow\overrightarrow{NP}=\frac{1}{2}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{NP}=\overrightarrow{MQ}\)
Câu b đề sai, \(\overrightarrow{PQ}=\overrightarrow{NM}\) mới đúng

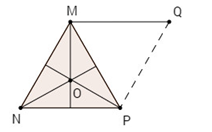
Vẽ −−→MQ=−−→NPMQ→=NP→
(MN→,NP→)=(MN→,MQ→)=120 độ.
Chọn (A).
Ngoài ra, có thể tính được:
(−−→MO,−−→ON)=60 độ \
(−−−→MN,−−→OP)=90 độ
(−−−→MN,−−→MP)=60 độ
ho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 12001200 ? (
A) (−−−→MN,−−→NP)(MN→,NP→);
(B) (−−→MO,−−→ON)(MO→,ON→);
(C) (−−−→MN,−−→OP)(MN→,OP→);
(D) (−−−→MN,−−→MP)(MN→,MP→).
#Tiểu Cừu

bài này là bài cơ bản, bạn nắm lí thuyết SGK là có thể làm được ( hình bạn tự vẽ nha)
Tam giác MNP có MN = MP suy ra tam giác MNP cân tại M
Xét tam giác MNI và MPI có MN = MP (gt) ; MI là cạnh chung và góc NMI = góc PMI
suy ra tam giác MNI = tam giác MPI (c-g-c)
b) Xét 2 tam giác vuông HNI và KPI có
IN = IP ( tam giác MNP cân suy ra phân giác đồng thời là trung tuyến )
góc HNI = góc KPI ( tam giác MNP cân tại M )
suy ra tam giác HNI = tam giác KPI ( cạnh huyền - góc nhọn )
a: Xét ΔMQN và ΔMQP có
MQ chung
\(\widehat{NMQ}=\widehat{PMQ}\)
NM=PM
Do đó: ΔMNQ=ΔMPQ
b: Ta có: ΔMNP cân tại M
mà MQ là phân giác
nên MQ là đường cao
c: NP=6cm nên NQ=3cm
=>MQ=4cm