

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



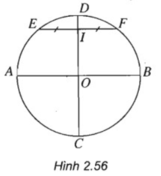
(h.2.56) Giả sử trên hình thực ta có đường tròn tâm O cùng với hai đường kính vuông góc của đường tròn đó là AB và CD. Nếu ta vẽ thêm một dây cung EF song song với AB thì đường kính CD sẽ đi qua trung điểm I của đoạn EF. Từ đó ta suy ra cách vẽ sau đây:
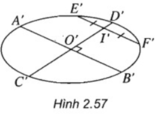
a) (h.2.57) Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính A'B' của hình elip đó. Đường kính này đi qua tâm O' của elip.
b) Vẽ một dây cung E'F' song song với đường kính A'B'. Gọi I' là trung điểm của E'F'. Đường thẳng O'I'cắt elip tại hai điểm C' và D'. Ta có A'B' và C'D' là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành A'C'B'D'là hình biểu diễn của hình vuông ACBD nội tiếp trong một đường tròn.

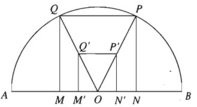
Gọi O là trung điểm của AB. Giả sử dựng được hình vuông MNPQ có M, N thuộc đường kính AB; P, Q thuộc nửa đường tròn. Khi đó O phải là trung điểm của MN. Nếu lấy một hình vuông M'N'P'Q' sao cho M', N' thuộc AB, O là trung điểm của M'N' thì dễ thấy
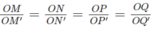
Từ đó suy ra hình vuông MNPQ là ảnh của hình vuông M'N'P'Q' qua phép vị tự tâm O, suy ra O, P, P' và O, Q, Q' thẳng hàng. Vậy ta có cách dựng:
- Dựng hình vuông M'N'P'Q' nằm trong nửa hình tròn đã cho sao cho M'N' thuộc AB và O là trung điểm của M'N'. Tia OP' cắt nửa đường tròn tại P; tia OQ' cắt nửa đường tròn tại Q.
Khi đó dễ thấy tứ giác MNPQ là hình vuông cần dựng


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).

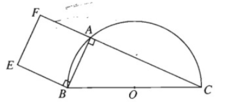
Xem E là ảnh của A qua phép quay tâm B, góc 90 ο . Khi A chạy trên nửa đường tròn (O), E sẽ chạy trên nửa đường tròn (O') là ảnh của nửa đường tròn (O) qua phép quay tâm tâm B, góc 90 ο .