Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

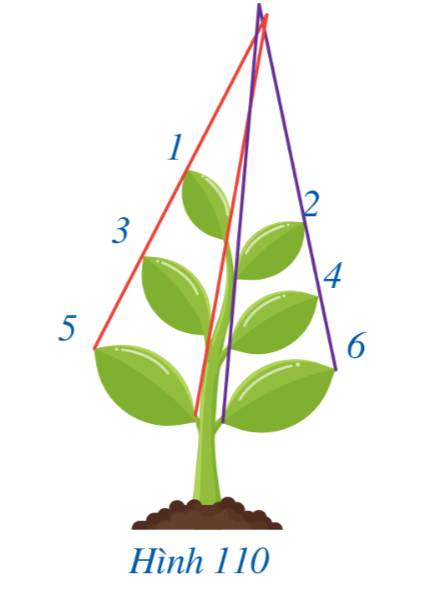
6 cặp lá mầm gợi nên những hình đồng dạng là:
- Lá 1 và 3
- Lá 3 và 5
- Lá 1 và 5
- Lá 2 và 4
- Lá 4 và 6
- Lá 2 và 6

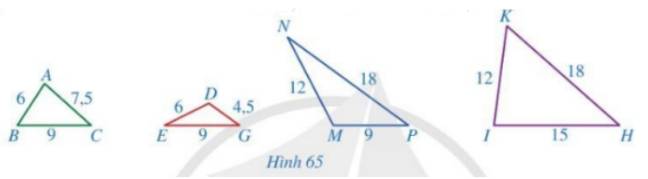
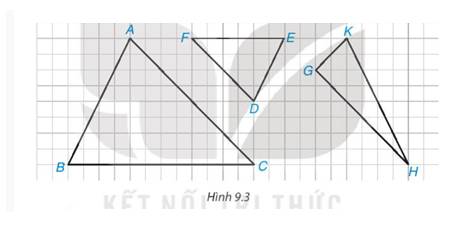
Xét tam giác ABC và tam giác IKH có:
\(\frac{{AB}}{{IK}} = \frac{{AC}}{{IH}} = \frac{{BC}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta ABC \backsim\Delta IKH\) (c-c-c)
Xét tam giác DEG và tam giác MNP có:
\(\frac{{DE}}{{MN}} = \frac{{DG}}{{MP}} = \frac{{EG}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta DEG \backsim\Delta MNP\) (c-c-c)

Học sinh thực hiện theo hướng dẫn của GV và SGK.
Ta có thể gấp và cắt giấy thành những chữ cái in hoa đồng dạng với nhau khác như:


Xét tam giác MPN có: \(\widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {60^o} - {70^o} = {50^o}\)
Các cặp tam giác đồng dạng trong hình 9.22 là: \(\Delta ACB \backsim \Delta DF{\rm{E; }}\Delta {\rm{ACB}} \backsim \Delta {\rm{MP}}N;\Delta DF{\rm{E}} \backsim \Delta MPN\)

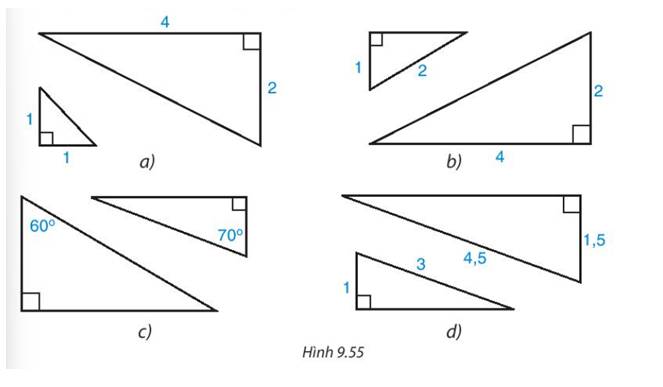
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

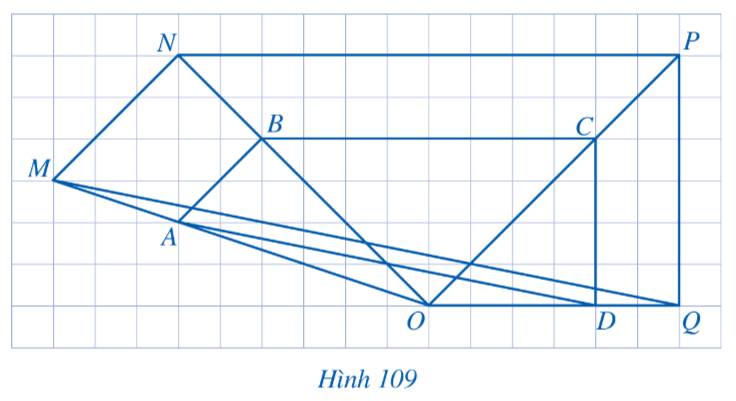
a) Tam giác OMN đồng dạng phối cảnh với tam giác OAB.
b) Tam giác ONP đồng dạng phối cảnh với tam giác OBC.
c) Tam giác OPQ đồng dạng phối cảnh với tam giác OCD.
d) Tứ giác MNPQ đồng dạng phối cảnh với tứ giác ABCD.

ΔABC \(\backsim\) ΔDEF với tỉ số đồng dạng là \(\frac{1}{2}\)

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)
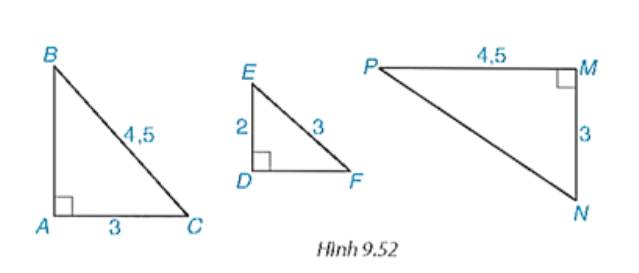





Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)