Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ dao động điều hoà với chu kì 2 s nên tần số góc là: ω=π(rad/s)
Động năng và thế năng bằng nhau lần thứ nhất thì:
Wt=Wd⇒\(\frac{1}{2}\)mω2A2cos2(ωt+φ0)= \(\frac{1}{2}\)mω2A2sin2(ωt+φ0)
⇒cos2(πt+φ0)=sin2(πt+φ0)
⇒πt+φ0=\(\frac{\pi }{4} + \frac{{k\pi }}{2}\)
Lần thứ nhất động năng và thế năng bằng nhau nên k=1,t=0 nên ta có: φ0=\(\frac{{3\pi }}{4}\)
Động năng và thế năng bằng nhau lần thứ hai sau khoảng thời gian:
πt+\(\frac{{3\pi }}{4}\)=\(\frac{\pi }{4} + \frac{{2\pi }}{2}\)⇒t=0,5s

a) Ta có:
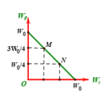
\(x=\dfrac{A}{2}=\dfrac{W_t}{W}=\dfrac{\dfrac{1}{2}mw^2x^2}{\dfrac{1}{2}mw^2A^2}=\dfrac{1}{4}\)
\(\Rightarrow W_t=25\%W\) và \(W_đ=75\%W\)
b) Mà:
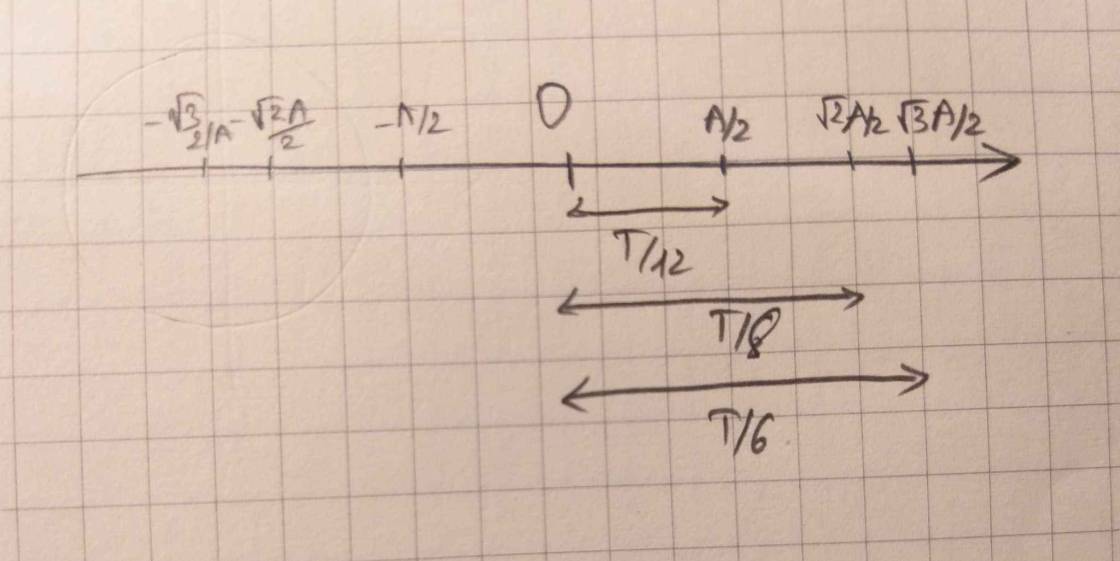
\(W_t=W_đ\Rightarrow\dfrac{W_t}{W}=\dfrac{\dfrac{1}{2}mw^2x^2}{\dfrac{1}{2}mw^2A^2}=\dfrac{1}{2}\)
\(\Rightarrow x=\pm\dfrac{A}{\sqrt{2}}\)

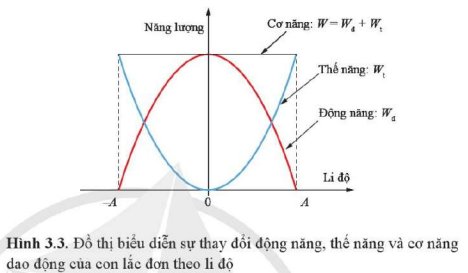
- Khi vật đi từ vị trí biên về vị trí cân bằng, thế năng của con lắc đơn giảm dần từ giá trị cực đại (bằng cơ năng của con lắc) về 0 (Mốc thế năng tại vị trí cân bằng). Do cơ năng của con lắc được bảo toàn, tổng của động năng và thế năng không đổi nên thế năng giảm bao nhiêu, động năng tăng bấy nhiêu. Do đó, khi vật đi từ biên về vị trí cân bằng, động năng của vật tăng từ 0 đến cực đại.
- Khi vật đi từ vị trí cân bằng về vị trí biên, thế năng của con lắc tăng dần từ 0 đến cực đại, trong khi động năng giảm dần từ cực đại về 0.

a) thế năng tăng dần trong khi động năng giảm dần là quá trình vật dao động từ vị trí cân bằng về hai biên.
b) thế năng giảm dần trong khi động năng tăng dần là quá trình vật dao động từ vị trí biên về vị trí cân bằng.

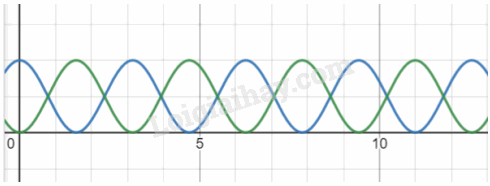
Phương trình dao động của vật là: \(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
Thế năng của dao động là: \(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t-\dfrac{\pi}{2}\right)\)
Động năng của dao động là: \(W_d=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t-\dfrac{\pi}{2}\right)\)
Đường màu xanh lá cây là thế năng, đường màu xanh nước biển là động năng
Trên đồ thị những thời điểm mà hai đồ thị cắt nhau thì động năng và thế năng có độ lớn bằng nhau

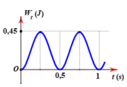
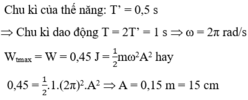
Phát biểu nào sau đây là sai khi nói về năng lượng của hệ dao động điều hoà:
A. Hệ có thế năng cực đại khi vật ở vị trí biên dương.
B. Vật có động năng cực đại khi ở vị trí cân bằng.
C. Hệ có cơ năng không đổi trong suốt quá trình dao động.
D. Hệ có thế năng bằng không khi vật ở vị trí biên âm
Hệ có động năng cực đại tại VTCB, thế năng cực đại tại vị trí hai biên (biên âm và dương) và ngược lại.