Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tỉ số giữa độ phóng xạ sau 11,4 ngày và độ phóng xạ ban đầu
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}=2^{-\frac{11,4}{3,8}}= 0,125. \)
=> Độ phóng xạ sau 11,4 ngày chiếm 12,5 % độ phóng xạ ban đầu

Ho = 14 hạt/phút

Số hạt nhân ban đầu
\(N_0= \frac{H_0}{\lambda}\)
Khối lượng ứng cới độ phóng xạ \(H_0\) là
\(m_0 = nA= \frac{N_0}{N_A}A= \frac{H_0}{N_A}= \frac{5.3,7.10^{10}.14}{6,02.10^{23} \frac{\ln 2}{5570.365.24.3600}}= 1,09g.\)

\(H=H_02^{-\frac{t}{T}}\)
=> \(\frac{H}{H_0}=32^{-1}= 2^{-5}= 2^{-\frac{t}{T}}\)
=> \(t = 5T= 690.\)(ngày)

t = 0 lúc mới chặt hiện tại t thời gian
Xét tỉ số giữa độ phóng xạ ở thời điểm \(t\) và độ phóng xạ ban đầu ( không cần chuyển đơn vị của độ phóng xạ từ phân rã / phút sang phân rã / giây vì dùng phép chia hai độ phóng xạ cho nhau.)
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}= \frac{1}{8}= 2^{-3}.\)
=> \(t = 3T= 3.5730 = 17190 \)(năm).

Khối lượng chất phóng xạ đã bị phân rã là
\(\Delta m = m_0(1-2^{-\frac{t}{T}}) \)
=> \(\frac{\Delta m }{m_0}= 0,75 =1- 2^{-\frac{t}{T}}\)
=> \(t = -T\ln_20,25 = 30h.\)

Đáp án A
Ta có:
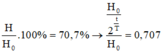
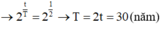
• Khối lượng ban đầu của chất phóng xạ:
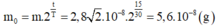
• Độ phóng xạ ban đầu:
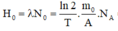


Khối lượng Rn còn lại sau 1,5 chu kì là: \(m=m_0.2^{-1,5}=2.2^{-1,5}(g)\)
Độ phóng xạ là: \(H=N.\lambda=\dfrac{2.2^{-1,5}}{222}.6,02.10^{23}.\dfrac{\ln 2}{3,8.24.3600}=...\)

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)
Đáp ánD