Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính chất:
- Hình bình hành:
Trong hình bình hành:
a) Các cạnh đối bằng nhau.
b) Các góc đối bằng nhau.
c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Hình chữ nhật:
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Hình thoi:
Trong hình thoi:
a) Hai đường chéo vuông góc với nhau.
b) Hai đường chéo là các đường phân giác của các góc của hình thoi.
- Hình vuông:
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

- Hình bình hành là tứ giác có các cạnh đối song song.
- Hình chữ nhật là tứ giác có bốn góc vuông.
- Hình thoi là tứ giác có bốn cạnh bằng nhau.
- Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.
Cách của tớ giống việt anh
a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.

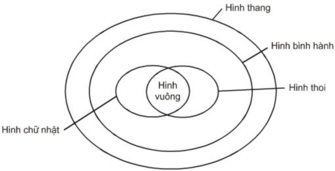
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang.
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang.
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.

a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình là hình bình hành và hình thang.
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình là hình bình hành và hình thang.
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình: hình vuông.

a) Tập hợp các hình chữ nhật là tập hợp con của các hình bình hành, hình thang.
b) Tập hợp các hình thoi là tập hợp con của các hình bình hành, hình thang.
c) Giao giữa tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.


- Hình chữ nhật có tính chất :
- Hình bình hành có tính chất: