Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nBaCO3=0,1(mol) ; nCo2=0,5(mol)
nBa2+=0,2(mol);nOH-=0,4+0,2a(mol)
nkết tủa theo Ba2+=0,2 mol >nBa thực tế nên kết tủa tan một phần
Ba(oh)2+co2-->Baco3+h2o
0,2---------0,2------0,2
KOH+co2-->KHco3
0,2a---0,2a----0,2a
Baco3+h2o +co2-->Ba(hco3)2
0,1-------------0,1
từ đó nco2=0,3+0,2a=0,5---->a=1M
tư

Đáp án A
nCO32- = nOH- - nCO2 = 0,25 – 0,2 = 0,05 mà nBa2+ = 0,1=> mBaCO3↓ = 0,05.197 = 9,85g Chọn A.

Ta có: \(\left\{{}\begin{matrix}n_{NaOH}=0,5.0,5=0,25\left(mol\right)\\n_{KOH}=0,5.0,5=0,25\left(mol\right)\\n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\end{matrix}\right.\)
Đặt CT chung của NaOH và KOH là AOH
=> \(n_{AOH}=n_{NaOH}+n_{KOH}=0,25+0,25=0,5\left(mol\right)\)
PTHH: 2AOH + CO2 \(\rightarrow\) A2CO3 + H2O
Ban đầu: 0,5 0,4
Pư: 0,5----->0,25
Sau pư: 0 0,15 0,25
A2CO3 + CO2 + H2O \(\rightarrow\) 2AHCO3
Ban đầu: 0,25 0,15
Pư: 0,15<----0,15
Sau pư: 0,1 0 0,3
=> \(\dfrac{1}{2}\) ddY có: \(\left\{{}\begin{matrix}n_{A_2CO_3}=\dfrac{0,1}{2}=0,05\left(mol\right)\\n_{AHCO_3}=\dfrac{0,3}{2}=0,15\left(mol\right)\end{matrix}\right.\)
PTHH: \(A_2CO_3+Ba\left(OH\right)_2\rightarrow BaCO_3\downarrow+2AOH\)
0,05--------------------->0,05
\(AHCO_3+Ba\left(OH\right)_{2\left(d\text{ư}\right)}\rightarrow BaCO_3\downarrow+AOH+H_2O\)
0,15-------------------------->0,15
\(A_2CO_3+BaCl_2\rightarrow BaCO_3\downarrow+2ACl\)
0,05------------------->0,05
=> \(\left\{{}\begin{matrix}a=\left(0,15+0,05\right).197=39,4\left(g\right)\\b=0,05.197=9,85\left(g\right)\end{matrix}\right.\)
=> a - b = 39,4 - 9,85 = 29,55 (g)

Chọn đáp án C
+ Lúc đầu, 0,1 mol CO2 chuyển Ba(OH)2 thành BaCO3.
+ Sau đó, 0,05 mol CO2 chuyển NaOH thành NaHCO3.
+ Còn lại 0,05 mol CO2 hòa tan 0,05 mol kết tủa, như vậy còn lại 0,05 mol BaCO3
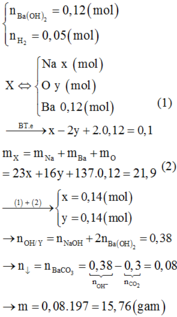

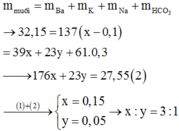
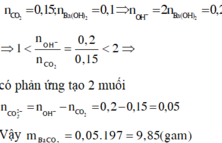
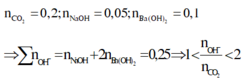

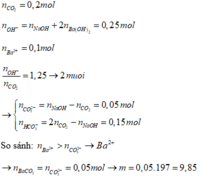
$n_{BaCO_3} = 0,1(mol) \Rightarrow n_{CO_3^{2-}} = n_{BaCO_3} = 0,1(mol)$
$n_{CO_2} = \dfrac{11,2}{22,4} = 0,5(mol)$
Suy ra : $n_{HCO_3^-} = 0,5 - 0,1 = 0,4(mol)$
Mà :
$n_{OH^-} = 2n_{CO_3^{2-}} + n_{HCO_3^-} = 0,1.2 + 0,4 = 0,6(mol)$
Suy ra: $0,6 = 0,2a + 0,2.1.2 \Rightarrow a = 1(M)$