Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi a = 2, ta có hệ phương trình
![]()
![]()
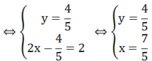
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7/5; 4/5)

a)

Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (1; -3)

x - 3 2 + x + 4 2 = 23 - 3x
⇔ x 2 - 6x + 9 + x 2 + 8x + 16 = 23 - 3x
⇔ 2 x 2 + 5x - 2 = 0
Ta có: a = 2; b = 5; c = -2
Δ = b 2 - 4ac = 5 2 - 4.2.(-2) = 41 > 0
⇒ phương trình đã cho có 2 nghiệm phân biệt
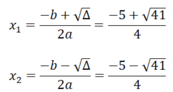
Vậy tập nghiệm của phương trình là
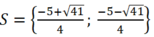

a) Ta có: a = 1; b’ = m + 3; c = m 2 + 3
Δ'= b ' 2 - ac = m + 3 2 - ( m 2 + 3) = m 2 + 6m + 9 - m 2 - 3 = 6m + 6

Thì phương trình thứ 2 các hệ số của x, y đều gấp 2 lần pt 1 mà VP phương trình 2 không gấp đôi VT pt 1 nên vô nghiệm chớ sao
Cả 2 chữ đều là VP hết nha. Viết láu táu nên ghi nhầm thành VT. Sorry nhá

Gọi chiều rộng sân trường là x (m)(x > 0)
Chiều dài sân trường là y (m) (y > x > 0)
Sân trường có chu vi là 340 m nên ta có : 2(x + y) = 340
Ba lần chiều dài hơn 4 lần chiều rộng là 20 m nên ta có: 3y – 4x = 20
Ta có hệ phương trình sau:
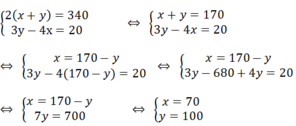
Vậy chiều dài là 100m; chiều rộng là 70m.
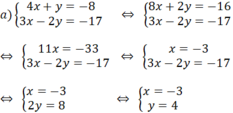
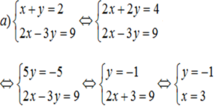
a) x 2 - 7x + 5 = 0
Δ = 7 2 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
Vậy hệ phương trình đã cho có tập nghiệm