Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=-5\\x=3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{2}\\x=3\end{cases}}\)
Vậy .........
\(b,\left(x^2-4\right)+\left(x-2\right)\left(3-2x=0\right)\)
\(\Leftrightarrow x^2-4-2x^2+7x-6=0\)
\(\Leftrightarrow-x^2+7x-10=0\)
\(\Leftrightarrow-\left(x-5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=2\end{cases}}\)
Vậy ..................
\(c,x^3-3x^2+3x-1=0\)
\(\Leftrightarrow\left(x-1\right)^3=0\)
\(\Leftrightarrow x=1\)
\(d,x\left(2x-7\right)-4x+14=0\)
\(\Leftrightarrow2x^2-7x-4x+14=0\)
\(\Leftrightarrow2x^2-11x+14=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{2}\\x=2\end{cases}}\)
Vậy ............
\(e,\left(2x-5\right)^2-\left(x+2\right)^2=0\)
\(\Leftrightarrow4x^2-20x+25-x^2-4x-4=0\)
\(\Leftrightarrow3x^2-24x+21=0\)
\(\Leftrightarrow3\left(x-7\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-7=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\x=1\end{cases}}\)
Vậy .....................
\(f,x^2-x-\left(3x-3\right)=0\)
\(\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x^2-4x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
Vậy ..............

bài 1:
a) ĐKXĐ: x khác 0; x khác -1
\(\frac{x-1}{x}+\frac{1-2x}{x^2+x}=\frac{1}{x+1}\)
<=> \(\frac{x-1}{x}+\frac{1-2x}{x\left(x+1\right)}=\frac{1}{x+1}\)
<=> (x - 1)(x + 1) + 1 - 2x = x
<=> x^2 - 2x = x
<=> x^2 - 2x - x = 0
<=> x^2 - 3x = 0
<=> x(x - 3) = 0
<=> x = 0 hoặc x - 3 = 0
<=> x = 0 hoặc x = 0 + 3
<=> x = 0 (ktm) hoặc x = 3 (tm)
=> x = 3
b) ĐKXĐ: x khác +-3; x khác -7/2
\(\frac{13}{\left(x-3\right)\left(2x+7\right)}+\frac{1}{2x+7}=\frac{6}{x^2-9}\)
<=> \(\frac{13}{\left(x-3\right)\left(2x+7\right)}+\frac{1}{2x+7}=\frac{6}{\left(x-3\right)\left(x+3\right)}\)
<=> 13(x + 3) + (x - 3)(x + 3) = 6(2x + 7)
<=> 13x + 30 + x^2 = 12x + 42
<=> 13x + 30 + x^2 - 12x - 42 = 0
<=> x - 12 + x^2 = 0
<=> (x - 3)(x + 4) = 0
<=> x - 3 = 0 hoặc x + 4 = 0
<=> x = 0 + 3 hoặc x = 0 - 4
<=> x = 3 (ktm) hoặc x = -4 (tm)
=> x = -4
c) ĐKXĐ: x khác +-1
\(\frac{x}{x-1}-\frac{2x}{\left(x-1\right)\left(x+1\right)}=0\)
<=> x(x + 1) - 2x = 0
<=> x^2 + x - 2x = 0
<=> x^2 - x = 0
<=> x(x - 1) = 0
<=> x = 0 hoặc x - 1 = 0
<=> x = 0 hoặc x = 0 + 1
<=> x = 0 (tm) hoặc x = 1 (ktm)
=> x = 0
d) \(\frac{x^2+2x}{x^2+1}-2x=0\)
<=> \(\frac{x\left(x+2\right)}{x^2+1}-2x=0\)
<=> x(x + 2) - 2x(x^2 + 1) = 0
<=> x^2 - 2x^3 = 0
<=> x^2(1 - 2x) = 0
<=> x^2 = 0 hoặc 1 - 2x = 0
<=> x = 0 hoặc -2x = 0 - 1
<=> x = 0 hoặc -2x = -1
<=> x = 0 hoặc x = 1/2
bài 2:
(x - 1)(x^2 + 3x - 2) - (x^3 - 1) = 0
<=> x^3 + 3x^2 - 2x - x^2 - 3x + 2 - x^2 + 1 = 0
<=> 2x^2 - 2x - 3x + 3 = 0
<=> 2x(x - 1) - 3(x - 1) = 0
<=> (2x - 3)(x - 1) = 0
<=> 2x - 3 = 0 hoặc x - 1 = 0
<=> 2x = 0 + 3 hoặc x = 0 + 1
<=> 2x = 3 hoặc x = 1
<=> x = 3/2 hoặc x = 1
bài 3:
(x^3 + x^2) + (x^2 + x) = 0
<=> x^3 + x^2 + x^2 + x = 0
<=> x^3 + 2x^2 + x = 0
<=> x(x^2 + 2x + 1) = 0
<=> x(x + 1)^2 = 0
<=> x = 0 hoặc x + 1 = 0
<=> x = 0 hoặc x = 0 - 1
<=> x = 0 hoặc x = -1

giải phương trình:
- Nếu \(x\ge1\)phương trình trở thành : \(x^2-3x+2=x-1\Leftrightarrow x^2-4x+3=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}TM}\)
- Nếu \(x< 1\)\(\Rightarrow x^2-3x+2=1-x\Leftrightarrow x^2-2x+1=0\Leftrightarrow\left(x-1\right)^2=0\Leftrightarrow x=1L\)VẬY NGHIỆM PHƯƠNG TRÌNH LÀ : x=1 hoặc x=3
\(x^4+2008x^2+2007x+2008\)
\(=x\left[x\left(x^2+2008\right)+2007\right]+2008\)
\(=\left[\left(x-1\right)x+2008\right]\left(x^2+x+1\right)\)
\(=\left(x^2-x+2008\right)\left(x^2+x+1\right)\)
~(‾▿‾~)

Trả lời:
1) sửa đề: \(x^4+x^3-4x-4=x^3\left(x+1\right)-4\left(x+1\right)=\left(x+1\right)\left(x^3-4\right)\)
2) \(x^2-\left(a+b\right)x+ab=x^2-ax-bx+ab=\left(x^2-ax\right)-\left(bx-ab\right)\)
\(=x\left(x-a\right)-b\left(x-a\right)=\left(x-a\right)\left(a-b\right)\)
3) \(5xy^3-2xyz-15y^2+6z=\left(5xy^3-15y^2\right)-\left(2xyz-6z\right)\)
\(=5y^2\left(xy-3\right)-2z\left(xy-3\right)=\left(xy-3\right)\left(5y^2-2z\right)\)

Mạnh dạn đưa pt 1 ẩn về 2 ẩn :)
Đặt \(\frac{x+3}{x-2}=u;\frac{x-3}{x+2}=v\)
Ta có:
\(u^2+6v=7uv\)
\(\Leftrightarrow\left(u-v\right)\left(u-6v\right)=0\)
Xét nốt nha!
Câu b là phân tích các kiểu ra dạng như thế này nhé !
\(\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
Hoặc là bạn dựa vào đó mà phân tích đến cái A là Ok

Câu 1:
a) \(2x^2+5x-3=\left(2x^2+6x\right)-\left(x+3\right)\)
\(=2x\left(x+3\right)-\left(x+3\right)=\left(x+3\right)\left(2x-1\right)\)
b) \(x^4+2009x^2+2008x+2009\)
\(=\left(x^4-x\right)+\left(2009x^2+2009x+2009\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)+2009\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+2009\right)\)
c) \(\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]=-16\) (đã sửa đề)
\(\Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16=0\)
\(\Leftrightarrow\left(x^2+10x+20\right)^2-16+16=0\)
\(\Leftrightarrow\left(x^2+10x+20\right)^2=0\)
\(\Leftrightarrow\left(x+5\right)^2-5=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-5-\sqrt{5}\\x=-5+\sqrt{5}\end{cases}}\)
Câu 1.
a) 2x2 + 5x - 3 = 2x2 + 6x - x - 3 = 2x( x + 3 ) - ( x + 3 ) = ( x + 3 )( 2x - 1 )
b) x4 + 2009x2 + 2008x + 2009
= x4 + 2009x2 + 2009x - x + 2009
= ( x4 - x ) + ( 2009x2 + 2009x + 2009 )
= x( x3 - 1 ) + 2009( x2 + x + 1 )
= x( x - 1 )( x2 + x + 1 ) + 2009( x2 + x + 1 )
= ( x2 + x + 1 )[ x( x - 1 ) + 2009 ]
= ( x2 + x + 1 )( x2 - x + 2009 )
c) ( x + 2 )( x + 4 )( x + 6 )( x + 8 ) = 16 ( xem lại đi chứ không phân tích được :v )
Câu 2.
3x2 + x - 6 - √2 = 0
<=> ( 3x2 - 6 ) + ( x - √2 ) = 0
<=> 3( x2 - 2 ) + ( x - √2 ) = 0
<=> 3( x - √2 )( x + √2 ) + ( x - √2 ) = 0
<=> ( x - √2 )[ 3( x + √2 ) + 1 ] = 0
<=> \(\orbr{\begin{cases}x-\sqrt{2}=0\\3\left(x+\sqrt{2}\right)+1=0\end{cases}}\)
+) x - √2 = 0 => x = √2
+) 3( x + √2 ) + 1 = 0
<=> 3( x + √2 ) = -1
<=> x + √2 = -1/3
<=> x = -1/3 - √2
Vậy S = { √2 ; -1/3 - √2 }
Câu 3.
A = x( x + 1 )( x2 + x - 4 )
= ( x2 + x )( x2 + x - 4 )
Đặt t = x2 + x
A = t( t - 4 ) = t2 - 4t = ( t2 - 4t + 4 ) - 4 = ( t - 2 )2 - 4 ≥ -4 ∀ t
Dấu "=" xảy ra khi t = 2
=> x2 + x = 2
=> x2 + x - 2 = 0
=> x2 - x + 2x - 2 = 0
=> x( x - 1 ) + 2( x - 1 ) = 0
=> ( x - 1 )( x + 2 ) = 0
=> x = 1 hoặc x = -2
=> MinA = -4 <=> x = 1 hoặc x = -2

1. \(B=\left(x-2\right)\left(x+2\right)\left(x+3\right)-\left(x+1\right)^3\)
\(=\left(x^2-4\right)\left(x+3\right)-\left(x^3+3x^2+3x+1\right)\)
\(=x^3+3x^2-4x-12-x^3-3x^2-3x-1\)
\(=-7x-13\)
2. \(64-x^2-y^2+2xy=64-\left(x^2+y^2-2xy\right)\)
\(=64-\left(x-y\right)^2=\left(8+x-y\right)\left(8-x+y\right)\)
3. \(2x^3-x^2+2x-1=0\)
\(\Leftrightarrow x^2.\left(2x-1\right)+\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+1\right)=0\)
Vì \(x^2\ge0\)\(\Rightarrow x^2+1>0\)
\(\Rightarrow2x-1=0\)\(\Rightarrow2x=1\)\(\Rightarrow x=\frac{1}{2}\)
Vậy \(x=\frac{1}{2}\)
Bài 1.
B = ( x - 2 )( x + 2 )( x + 3 ) - ( x + 1 )3
= ( x2 - 4 )( x + 3 ) - ( x3 + 3x2 + 3x + 1 )
= x3 + 3x2 - 4x - 12 - x3 - 3x2 - 3x - 1
= -7x - 13
Bài 2.
64 - x2 - y2 + 2xy
= 64 - ( x2 - 2xy + y2 )
= 82 - ( x - y )2
= ( 8 - x + y )( 8 + x - y )
Bài 3.
2x3 - x2 + 2x - 1 = 0
<=> ( 2x3 - x2 ) + ( 2x - 1 ) = 0
<=> x2( 2x - 1 ) + 1( 2x - 1 ) = 0
<=> ( 2x - 1 )( x2 + 1 ) = 0
<=> \(\orbr{\begin{cases}2x-1=0\\x^2+1=0\end{cases}}\Leftrightarrow x=\frac{1}{2}\)( vì x2 + 1 ≥ 1 > 0 ∀ x )

\(x^3-x^2-14x+24\)
\(=x^3-2x^2+x^2-2x-12x+24\)
\(=x^2\left(x-2\right)+x\left(x-2\right)-12\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+x-12\right)\)
\(=\left(x-2\right).\left[x^2+4x-3x-12\right]\)
\(=\left(x-2\right).\left[x\left(x+4\right)-3\left(x+4\right)\right]\)
\(=\left(x-2\right)\left(x+4\right)\left(x-3\right)\)
\(x^4+x^3+2x-4\)
\(=x^4-x^3+2x^3-2x^2+2x^2-2x+4x-4\)
\(=x^3\left(x-1\right)+2x^2\left(x-1\right)+2x\left(x-1\right)+4\left(x-1\right)\)
\(=\left(x-1\right)\left(x^3+2x^2+2x+4\right)\)
\(=\left(x-1\right).\left[x^2\left(x+2\right)+2\left(x+2\right)\right]\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+2\right)\)
\(8x^4-2x^3-3x^2-2x-1\)
\(=8x^4-8x^3+6x^3-6x^2+3x^2-3x+x-1\)
\(=8x^3\left(x-1\right)+6x^2\left(x-1\right)+3x\left(x-1\right)+x-1\)
\(=\left(x-1\right)\left(8x^3+6x^2+3x+1\right)\)
\(=\left(x-1\right)\left[\left(8x^3+1\right)+\left(6x^2+3x\right)\right]\)
\(=\left(x-1\right)\left[\left(2x+1\right)\left(4x^2-2x+1\right)+3x\left(2x+1\right)\right]\)
\(=\left(x-1\right)\left(2x+1\right)\left(4x^2+x+1\right)\)
\(3x^2-7x+2\)
\(=3x^2-6x-x+2\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
Chúc bạn học tốt.
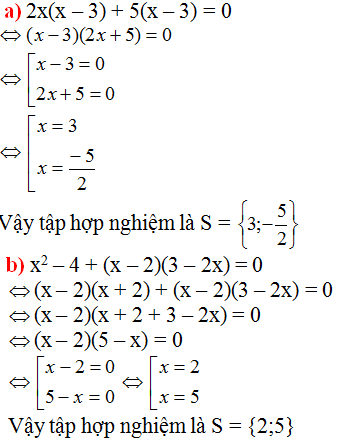
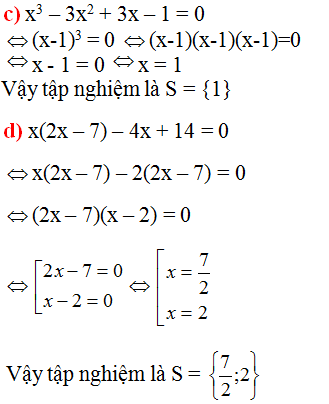
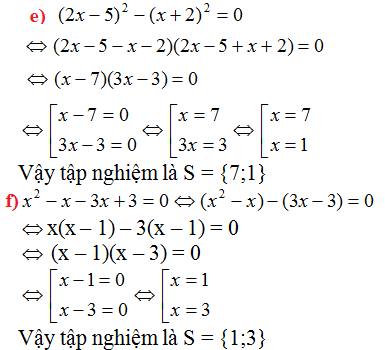
(x2 – 4) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)(x + 2) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)[(x + 2) + (3 – 2x)] = 0
⇔ (x – 2)(5 – x) = 0
⇔ x – 2 = 0 hoặc 5 – x = 0
+ x – 2 = 0 ⇔ x = 2
+ 5 – x = 0 ⇔ x = 5.
Vậy tập nghiệm của phương trình là S = {2; 5}.