CP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
22 tháng 10 2017
\(3x^4+6x^3-7x^2+8x-10\)
\(=\left(3x^4-3x^3\right)+\left(9x^3-9x^2\right)+\left(2x^2-2x\right)+\left(10x-10\right)\)
\(=\left(x-1\right)\left(3x^3+9x^2+2x+10\right)\)
N
19 tháng 12 2018
\(-3x^2-7x+10\)
\(=3x-3x^2+10-10x\)
\(=3x.\left(1-x\right)+10.\left(1-x\right)=\left(3x+10\right).\left(1-x\right)\)
19 tháng 12 2018
\(-3x^2+3y^2-4xz-4yz\)
\(=3\left(y^2-x^2\right)-4z\left(x+y\right)\)
\(=3\left(y-x\right)\left(x+y\right)-4z\left(x+y\right)\)
\(=\left(x+y\right)\left(3y-3x-4z\right)\)
PT
2
14 tháng 12 2016
\(7x-3x^2-2\)
\(=6x+x-3x^2-2\)
\(=\left(6x-3x^2\right)+\left(x-2\right)\)
\(=-3x\left(x-2\right)+\left(x-2\right)\)
\(=\left(-3x+1\right)\left(x-2\right)\)
13 tháng 8 2019
\(7x - 3x^2 - 2\)
\(= 6x + x - 3x^2 - 2\)
\(=(6x-3x^2)+(x-2)\)
\(= -3x(x-2)+(x-2)\)
\(=(-3x+1)(x-2)\)
PH
2 tháng 11 2017
a)\(\dfrac{3x^2-12x+12}{x^4-8x}=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x^3-2^3\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)
NN
3
KT
27 tháng 1 2018
\(3x^3-7x^2+17x-5\)
\(=3x^3-x^2-6x^2+2x+15x-5\)
\(=x^2\left(3x-1\right)-2x\left(3x-1\right)+5\left(3x-1\right)\)
\(=\left(3x-1\right)\left(x^2-2x+5\right)\)
27 tháng 1 2018
3x^3-7x^2+17x-5
= (3x^3-x^2)-(6x^2-2x)+(15x-5)
= (3x-1).(x^2-6x+15)
Tk mk nha
CM
1
FM
12 tháng 10 2018
Ta có:
\(2x^2-5xy+3y^2\)
\(=2x^2-2xy-3xy+3y^2=2x\left(x-y\right)-3y\left(x-y\right)\)
\(=\left(x-y\right)\left(2x-3y\right)\)
\(x^3-7x-6=x^3+1-7x-7\)
\(=\left(x+1\right)\left(x^2-x+1\right)-7\left(x+1\right)=\left(x+1\right)\left(x^2-x-6\right)\)
\(=\left(x+1\right)\left(x-3\right)\left(x+2\right)\)
30 tháng 6 2017
Ta có : \(4x^2-3x-1\)
\(=4x^2-4x+x-1\)
\(=4x\left(x-1\right)+\left(x-1\right)\)
\(=\left(x-1\right)\left(4x+1\right)\)
30 tháng 6 2017
Ta có : \(x^2-7x+12\)
\(=x^2-3x-4x+12\)
\(=x\left(x-3\right)-\left(4x-12\right)\)
\(=x\left(x-3\right)-4\left(x-3\right)\)
\(=\left(x-4\right)\left(x-3\right)\)
GF
1
HH
1
PA
15 tháng 11 2016
\(2x^4+3x^3-7x^2-6x+8\)
\(=2x^4+5x^3-2x^2-8x-2x^3-5x^2+2x+8\)
\(=x\left(2x^3+5x^2-2x-8\right)-\left(2x^3+5x^2-2x-8\right)\)
\(=\left(x-1\right)\left(2x^3+5x^2-2x-8\right)\)
\(=\left(x-1\right)\left(2x^3+x^2-4x+4x^2+2x-8\right)\)
\(=\left(x-1\right)\left[x\left(2x^2+x-4\right)+2\left(2x^2+x-4\right)\right]\)
\(=\left(x-1\right)\left(x+2\right)\left(2x^2+x-4\right)\)
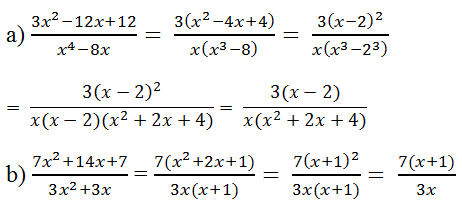
\(\Rightarrow3x^2-10x+3x-10\)
\(\Rightarrow x\left(3x-10\right)+\left(3x-10\right)\)
\(\Rightarrow\left(3x-10\right)\left(x+1\right)\)
T I C K nha cảm ơn rất nhìu