Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a^4+a^3+a^{3b}+a^{2b}\)
\(=a\left(a^3+a^2+1^{3b}+1^{2b}\right)\)
\(a^3+3a^2+4a+12\)
\(=a^2\left(a+3\right)+4\left(a+3\right)\)
\(=\left(a^2+4\right)\left(a+3\right)\)

b. \(\left(a^2+a\right)+a\left(a^2+a\right)-12\)
<=>\(\left(x^3+3x^2-4\right)+\left(3x^2+9x-12\right)\)
<=>\(x\left(x^2+3x-4\right)+3\left(x^2+3x-4\right)\)
<=>\(\left(x^2+3x-4\right)\left(x+3\right)\)
<=>\(\left(x+3\right)\left(x^2+4x\right)-\left(x-4\right)\)
đóngmở ngoặc nhé mk ngại ghi lại
<=>(x+3)(x(x+4)-(x+4))
<=>(x+3)(x-1)(x+4)
kết pn fb mk nhé longtrangv@gmail.com
c) \(x^3-x^2-4x^2+8x-4\)
= \(x^3-x^2-4x^2+4x+4x-4\)
= \(x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\)
= \(\left(x-1\right)\left(x^2-4x+4\right)\)
= \(\left(x-1\right)\left(x-2\right)^2\)

a) a2−b2−4a+4
=(a2-4a+4)-b2
=(a-2)2-b2
=(a-2-b)(a-2+b)a2−b2−4a+4
b) x2+2x−3
=x2-x+3x-3
=x(x-1)+3(x-1)
=(x+3)(x-1)x2+2x−3
c) 4x2y2−(x2+y2)2
=(2xy-x2-y2)(2xy+x2+y2)
=-(x-y)2(x+y)2
d) 2a3−54b3
=2(a3-27b3)
=2(a-3b)(a2+3ab+9b2)

a) 4a2b3 - 6a3b2 = 2a2b2( 2b - 3a )
b) ( a - b )2 - ( b - a ) = ( a - b )2 + ( a - b ) = ( a - b )( a - b + 1 )
c) ( 8a3 - 27b3 ) - 2a( 4a2 - 9b2 ) = 8a3 - 27b3 - 8a3 + 18ab2 = 18ab2 - 27b3 = 9b2( 2a - 3b )
d) 10x2 + 10xy + 5x + 5y = 10x( x + y ) + 5( x + y ) = ( x + y )( 10x + 5 ) = 5( x + y )( 2x + 1 )
e) 5ay - 3bx + ax - 15by = 5y( a - 3b ) + x( a - 3b ) = ( a - 3b )( 5y + x )
a) \(4a^2.b^3-6a^3.b^2=2a^2.b^2\left(2b-3a\right)\)
b) \(\left(a-b\right)^2-\left(b-a\right)=\left(a-b\right)^2+\left(a-b\right)\)
\(=\left(a-b\right).\left(a-b+1\right)\)
c) \(8a^3-27b^3-2a.\left(4a^2-9b^2\right)=8a^3-27b^3-8a^3+18ab^2\)
\(=-27b^3+18ab^2=18ab^2-27b^3=9b^2.\left(2a-3b\right)\)
d) \(10x^2+10xy+5x+5y=5.\left(2x^2+2xy+x+y\right)\)
\(=5.\left[\left(2x^2+2xy\right)+\left(x+y\right)\right]=5.\left[2x\left(x+y\right)+\left(x+y\right)\right]\)
\(=5\left(x+y\right)\left(2y+1\right)\)
e) \(5ay-3bx+ax-15by=\left(5ay-15by\right)-\left(3bx-ax\right)\)
\(=5y\left(a-3b\right)-x\left(3b-a\right)=5y\left(a-3b\right)+x\left(a-3b\right)\)
\(=\left(a-3b\right)\left(x+5y\right)\)

A/\(4x^2-12+9\)
\(=\left(2x\right)^2-2.2.3+3^2\)
\(=\left(2x+3\right)^2\)
B/\(11x+11y-x^2-xy\)
\(=\left(11x-x^2\right)+\left(11y-xy\right)\)
\(=x\left(11-x\right)+y\left(11-x\right)\)
\(=\left(11-x\right)\left(x+y\right)\)
C/\(4a^2b^2-\left(a^2+b^2-c^2\right)^2\)
\(=\left(2ab\right)^2-\left(a^2+b^2-c^2\right)^2\)
\(=\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)\)

a, x(a - b) + (a - b)
= (x + 1)(a - b)
b, x(a + b) - a - b
= x(a + b) - (a + b)
= (x - 1)(a + b)
c, 10ax - 5ay - 2x + y
= 5a(2x - y) - (2x - y)
= (5a - 1)(2x - y)
d, 2a^2x - 5by - 5a^2y + 2bx
= 2x(a^2 + b) - 5y(b + a^2)
= (2a - 5y)(a^2 + b)
làm tiếp:
2ax2 - bx2 - 2ax +bx +4a-2b
= x2(2a-b) - x(2a-b) +2(2a-b)
=(2a-b)(x2-x+2)

\(\left(a-b\right)^2-\left(b-a\right)\)
\(=\left(a-b\right)^2+\left(a-b\right)\)
\(=\left(a-b\right)\left(a-b+1\right)\)
\(5\left(a+b\right)^2-\left(a+b\right)\left(a-b\right)\)
\(=\left(a+b\right)\left[5\left(a+b\right)-\left(a-b\right)\right]\)
\(=\left(a+b\right)\left[5a+5b-a+b\right]\)
\(=\left(a+b\right)\left[4a+6b\right]\)

4a2b2-(a2+b2-c2)2
= (4ab-a2-b2+c2)(4ab+a2+b2-c2)
= -[(a-b)2-c2][(a+b)2-c2]
=-(a-b+c)(a-b-c)(a+b-c)(a+b+c)
=(b-a-c)(b+c-a)(a+b-c)(a+b+c)
\(4a^2b^2-\left(a^2+b^2-c^2\right)^2\)
\(=\left(2ab\right)^2-\left(a^2+b^2-c^2\right)^2\)
\(=\left(2ab-a^2-b^2+c^2\right)\left(2ab+a^2+b^2-c^2\right)\)
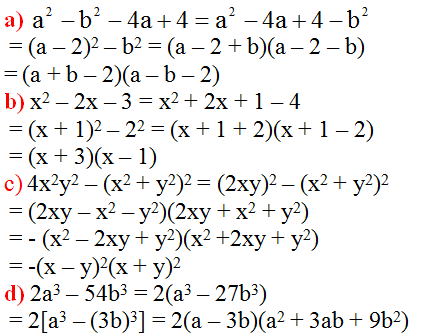
\(a^4+a^3+a^3b+a^2b\)
\(=a^2\left(a^2+a+b+b\right)\)
\(=a^2\left(a^2+a+2b\right)\)
\(a^3+4a^2+4a+3\)
a, \(a^4+a^3+a^3b+a^2b=a^3\left(a+1\right)+a^2b\left(a+1\right)=\left(a+1\right)\left(a^2b+a^3\right)=a^2\left(a+1\right)\left(b+a\right)\)