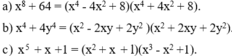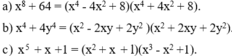
a)...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a)x3+x2+4 =x3-x2+2x+2x2-2x+4 =x(x2-x+2)+2(x2-x+2) =(x+2)(x2-x+2) b)x3-2x-4 =x3+2x2+2x-2x2-4x-4 =x(x2+2x+2)-2(x2+2x+2) =(x-2)(x2+2x+2) \(x^4+x^2+x\) \(=x^2+x+x^4\) \(=x^2+2x.\frac{1}{2}+\frac{1}{2}^2-\frac{1}{2}^2+x^4\) \(=\left(x^2+2x.\frac{1}{2}+\frac{1}{2}^2\right)-\frac{1}{2}^2+x^4\) \(=\left(x+\frac{1}{2}\right)^2-\frac{1}{2}^2+x^4\) \(=\left(x+\frac{1}{2}\right)^2-\frac{1}{4}+x^4\) \(=\left(x+\frac{1}{2}\right)^2-\sqrt{\frac{1}{4}}^2+x^4\) \(=\left(x+\frac{1}{2}-\sqrt{\frac{1}{4}}\right).\left(x+\frac{1}{2}+\sqrt{\frac{1}{4}}\right)+x^4\) Đến đây dễ rồi .Biến đổi ngoặc bên phải giống ngoặc trái rồi mở ngoặc đặt nhân tử chung là được . x^4+4=x^4 + 4x^2 +4 - 4x^2=(x^2)^2+ 2.x^2.2+2^2 - (2x)^2 = (x^2+2)-(2x)^2 =(x^2+2-2x)(2^2+2-2x) \(x^4+4=x^4+4x^2+4-4x^2\) \(=\left(x^2+2\right)^2-4x^2\) \(=\left(x^2+2-2x\right)\left(x^2+2+2x\right)\) a)2x2+3x-5 =2x2+5x-2x-5 =x(2x+5)-(2x+5) =(x-1)(2x+5) b)x8+x4+1 =(x4)2+2x4+1-x4 =(x4+1)2-x4 =(x4+1-x2)(x4+x2+1) =(x4-x2+1)(x2-x+1)(x2+x+1) a, \(=x^5+x^4+x^3-x^4-x^3-x^2+x^2+x+1\) \(=x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\) \(=\left(x^2+x+1\right)\left(x^3-x^2+1\right)\)
K
Khách
CM
Cao Minh Tâm
29 tháng 11 2019
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
2
NH
1
TN
2 tháng 11 2016
23 tháng 7 2018
TN
28 tháng 10 2017
28 tháng 10 2017
LV
1
TN
25 tháng 7 2016
15 tháng 9 2017
