Phân tích các đa thức sau thành nhân tử x 2 + 4 x - y 2 + 4 </spa...

Phân tích các đa thức sau thành nhân tử x 2 + 4 x...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

23 tháng 8 2017

Phân tích các đa thức sau thành nhân tử x 2 + 4 x - y 2 + 4 .

#Toán lớp 8

Cao Minh Tâm

23 tháng 8 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Mây

8 tháng 8 2018 - olm

phân tích các đa thức sau thành nhân tử

\(x^2+4x-y^2+4\)

#Toán lớp 8

kudo shinichi

8 tháng 8 2018

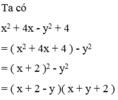
\(x^2+4x-y^2+4\)

\(=\left(x^2+2.x.2+2^2\right)-y^2\)

\(=\left(x+2\right)^2-y^2\)

\(=\left(x+2-y\right).\left(x+2+y\right)\)

Tham khảo nhé~

Đúng(0)

Trần Thùy Dương

8 tháng 8 2018

\(x^2+4x-y^2+4\)

\(=x^2+4x+4-y^2\)

\(=\left(x^2+4x+4\right)-y^2\)

\(=\left(x^2+2x.2+2^2\right)-y^2\)

\(=\left(x+2\right)^2-y^2\)

\(=\left[\left(x+2\right)+y^2\right].\left[\left(x+2\right)-y^2\right]\)

\(=\left(x+2+y^2\right)\left(x+3-y^2\right)\)

Đúng(0)

Công chúa thủy tề

31 tháng 7 2018 - olm

Phân tích các đa thức sau thành nhân tử:

\(e,x^2+y^2-x^2y^2+xy-x-y\)

\(f,x^4+2x^3-4x-4\)

#Toán lớp 8

mạnh lê

1 tháng 8 2018

x²⁺y²-x²y²+xy-x-y=x²-x²y²+y²-y-x+xy

=x(1-y²)+y(y-1)-x(1-y)

=x²(y-1)(y+1)+y(y-1)+x(y-1)

=-x²(y-1)(y+1)+y(y-1)+x(y-1)

=(y-1)(-x²(y+1)+y+x)

Đúng(0)

mạnh lê

1 tháng 8 2018

f) x⁴+2x²-4x-4=(x³.x+x³.2)-(2x.2+2.2)

=x³(x+2)-2(x+2)

=(x³-2)(x+2)

Đúng(0)

Kim Jennie

5 tháng 10 2020 - olm

Phân tích các đa thức sau thành nhân tử(sử dụng các hằng đẳng thức)

a)\(16x^2-\left(x^2+4\right)^2\)

b)\(\left(x+y\right)^3+\left(x-y\right)^3\)

#Toán lớp 8

l҉o҉n҉g҉ d҉z҉

5 tháng 10 2020

a) 16x² - ( x² + 4 )²

= ( 4x )² - ( x² + 4 )²

= [ 4x - ( x² + 4 ) ][ 4x + ( x² + 4 ) ]

= ( -x² + 4x - 4 )( x² + 4x + 4 )

= [ -( x² - 4x + 4 ) ]( x + 2 )²

= [ -( x - 2 )² ]( x + 2 )²

b) ( x + y )³ + ( x - y )³

= [ ( x + y ) + ( x - y ) ][ ( x + y )² - ( x + y )( x - y ) + ( x - y )² ]

= ( x + y + x - y )[ x² + 2xy + y² - ( x² - y² ) + x² - 2xy + y² ]

= 2x( 2x² + 2y² - x² + y²

= 2x( x² + 3y² )

Đúng(0)

Nguyễn Phương Thảo

4 tháng 7 2017 - olm

Phân tích đa thức sau thành nhân tử: x^2-4(x^2)(y^2) + y^2 +2xy

#Toán lớp 8

Hoàng Thị Lan Hương

4 tháng 7 2017

\(=\left(x^2+2xy+y^2\right)-4x^2y^2\)

\(=\left(x+y\right)^2-\left(2xy\right)^2\)

\(=\left(x+y+2xy\right)\left(x+y-2xy\right)\)

Đúng(0)

Trần Thị Thùy Linh 2004

4 tháng 7 2017

x² -4x²y² +y² +2xy =( x² +2xy +y²) -(2xy)² =(x+y)² -(2xy)²=(x+y+2xy)(x+y-2xy)

Đúng(0)

Trần Linh Trang

6 tháng 9 2016 - olm

phân tích đa thức sau thành nhân tử: \(\left(x-y\right)^2+4\left(x-y\right)-12\)

#Toán lớp 8

Mai Thanh

2 tháng 8 2018 - olm

Phân tích các đa thức sau thành nhân tử:

a) \(x^4-4x^2+4x-1\)

b) \(x^2\left(x^2+4\right)-x^2+4\)

#Toán lớp 8

Bang Bang 2

2 tháng 8 2018

Bài làm ai trên 11 điểm tích mình thì mình tích lại

Ông tùng hơn tùng số tuổi là :

29 + 32 = 61 (tuổi )

Vậy ông của tùng hơn tùng 61 tuổi

Đúng(0)

lisablackpink

2 tháng 8 2018

We .........(have) an English lesson on Monday

Đúng(0)

Mai Thanh

2 tháng 8 2018 - olm

Phân tích các đa thức sau thành nhân tử:

\(x^2\left(x+4\right)^2-\left(x+4\right)^2-\left(x^2-1\right)\)

#Toán lớp 8

Lê Ng Hải Anh

2 tháng 8 2018

\(x^2\left(x+4\right)^2-\left(x+4\right)^2-\left(x^2-1\right)\)

\(=\left(x+4\right)^2\left(x^2-1\right)-\left(x^2-1\right)\)

\(=\left(x^2-1\right)\left[\left(x+4\right)^2-1\right]\)

\(=\left(x-1\right)\left(x+1\right)\left(x+4+1\right)\left(x+4-1\right)\)

\(=\left(x-1\right)\left(x+1\right)\left(x+5\right)\left(x-3\right)\)

=.= hok tốt!!

Đúng(0)

Phạm Thị Thu Trang

18 tháng 8 2016 - olm

Phân tích đa thức thành nhân tử :

\(F=x^2-4^x+4-y^2\)

#Toán lớp 8

Phạm Thị Thu Trang

18 tháng 8 2016

Ta có : \(F=x^2-4^x+4-y^2\)

\(=\left(x^2-4^x+4\right)-y^2\)( nhóm hạng tử )

\(=\left(x-2\right)^2-y^2\)( đẳng thức số 2 )

\(=\left(x-2-y\right)\left(x-2+y\right)\)( đẳng thức số 3 )

Vậy : \(F=\left(x-2-y\right)\left(x-2+y\right)\)

Đúng(0)

JOKER_Võ Văn Quốc

18 tháng 8 2016

=(x-2)²-y²=(x-y-2)(x+y-2)

Đúng(0)

Đăng Trần Hải

12 tháng 2 2020 - olm

phân tích đa thức sau thành nhân tử:

\(^{x^2\left(x^2+4\right)-x^2+4}\)

#Toán lớp 8

Inequalities

12 tháng 2 2020

\(x^2\left(x^2+4\right)-x^2+4\)

\(=x^4+4x^2-x^2+4\)

\(=x^4+3x^2+4\)

\(=x^4-x^3+x^3+2x^2+2x^2-x^2-2x+2x+4\)

\(=\left(x^4-x^3+2x^2\right)+\left(x^3-x^2+2x\right)+\left(2x^2-2x+4\right)\)

\(=x^2\left(x^2-x+2\right)+x\left(x^2-x+2\right)+2\left(x^2-x+2\right)\)

\(=\left(x^2+x+2\right)\left(x^2-x+2\right)\)

Đúng(0)

Công chúa thủy tề

26 tháng 7 2018 - olm

Phân tích các đa thức sau thành nhân tử:

\(h,x^4+4\)

\(i,\left(1+x^2\right)^2-4x\left(1-x^2\right)\)

#Toán lớp 8

KAl(SO4)2·12H2O

26 tháng 7 2018

h) \(x^4+4=\left(x^2+2x+2\right)\left(x^2-2x+2\right)\)

i) \(\left(1+x^2\right)^2-4x\left(1-x^2\right)=\left(1+x^2\right)^2+4x^3-4x=x^4+4x^3+2x^2-4x+1\)

Đúng(0)

Bích Trịnh

26 tháng 7 2018

x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=(x^2+2-2x)(x^2+2+2x)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP