
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Có \(\widehat{OAM}=90^0\) => Tam giác \(OAM\) nội tiếp đường tròn đường kính OM
=> O,A,M cùng thuộc đường tròn đường kính OM (*)
Có \(\widehat{OBM}=90^0\) => Tam giác \(OBM\) nội tiếp đường tròn đường kính OM
=> O,B,M cùng thuộc đường tròn đường kính OM (2*)
Do N là trung điểm của PQ => \(ON\perp PQ\)( Vì trong một đt, đường kính đi qua trung điểm của một dây ko đi qua tâm thì vuông góc với dây ấy)
=> \(\widehat{ONM}=90^0\) => Tam giác \(ONM\) nội tiếp đường tròn đường kính OM
=> O,N,M cùng thuộc đt đường kính OM (3*)
Từ (*) (2*) (3*) => O,M,N,A,B cùng thuộc đt đk OM hay đt bán kính \(\dfrac{OM}{2}\)
b) Có AM//PS (cùng vuông góc với OA)
Gọi E là gđ của PS với (O) => \(sđ\stackrel\frown{AE}=sđ\stackrel\frown{AP}\)
Có \(\widehat{PRB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AE}+sđ\stackrel\frown{PB}\right)\)\(=\dfrac{1}{2}\left(sđ\stackrel\frown{AP}+sđ\stackrel\frown{PB}\right)=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
=> \(\widehat{PRB}=\widehat{MAB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
Có BNAM nội tiếp => \(\widehat{MAB}=\widehat{MNB}\)
\(\Rightarrow\widehat{PRB}=\widehat{MNP}\) => PRNB nội tiếp
\(\Rightarrow\widehat{BRN}=\widehat{BPN}\) mà \(\widehat{BPN}=\widehat{BAQ}=\dfrac{1}{2}sđ\stackrel\frown{BQ}\)
\(\Rightarrow\widehat{BRN}=\widehat{BAQ}\) => RN//AQ hay RN // SQ mà N la trung điểm của PQ
=> RN là đường TB của tam giác PSQ
=> R là trung điểm của PS <=> PR=RS

\(P=A.B=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}.\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\)
\(=1+\dfrac{9}{\sqrt{x}-3}\le1+\dfrac{9}{0-3}=1-3=-2\)
\(maxP=-2\Leftrightarrow x=0\)
\(1,x=16\Leftrightarrow A=\dfrac{4-1}{4-3}=\dfrac{3}{1}=3\\ 2,B=\dfrac{x+2\sqrt{x}-3+5\sqrt{x}+5+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\\ 3,P=AB=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\\ P=1+\dfrac{9}{\sqrt{x}-3}\\ Vì.\sqrt{x}-3\ge-3\Leftrightarrow\dfrac{9}{\sqrt{x}-3}\le-3\\ \Leftrightarrow P=1+\dfrac{9}{\sqrt{x}-3}\le1-3=-2\\ P_{max}=-2\Leftrightarrow x=0\)


a) Tam giác OAC là tam giác vuông. Vì AC là đường cao của tam giác vuông OAC, và đường cao luôn vuông góc với cạnh đối diện nên tam giác OAC là tam giác vuông tại A. b) Ta có CH vuông góc với AB tại H và AC vuông góc với BC. Theo định lý Euclid, trong một tam giác vuông, bình phương của độ dài đường cao bằng tích của độ dài đoạn thẳng từ đỉnh vuông góc đến điểm chia cạnh huyền. Vì vậy, CH^2 = AH * HB. c) Vì K là trung điểm của BC, nên BK = KC. Do đó, K nằm trên đường tròn (O) với đường kính BC. d) Gọi I là trung điểm của CH. Ta biết rằng AI là đường phân giác của góc OAC. Vì OAC là tam giác vuông tại A, nên AI cũng là đường phân giác của góc OAB. Do đó, AI cắt đường tròn (O) tại một điểm E. Để tính AE.BD + OK.OD, ta cần biết thêm thông tin về vị trí của các điểm A, B, C, D, E, O, K và H trên đường tròn (O) và tam giác OAC.
______________________HT____________________________

a)\(\Rightarrow P=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
b) Ta có P=2
\(\dfrac{\Leftrightarrow3\sqrt{x}}{\sqrt{x}+2}=2\Leftrightarrow3\sqrt{x}=2\sqrt{x}+4\)
\(\Leftrightarrow\sqrt{x}=4\Leftrightarrow x=16\left(n\right)\)
Vậy x=16 thì P=2

a: E đối xứng B qua AH
=>AH là trung trực của BE
=>AH\(\perp\)BE tại trung điểm của BE
Ta có: AH\(\perp\)BE
AH\(\perp\)BC
BE,BC có điểm chung là B
Do đó: B,E,C thẳng hàng
=>AH\(\perp\)BC tại trung điểm của BE
=>H là trung điểm của BE
D đối xứng A qua BC
=>BC là đường trung trực của AD
=>BC\(\perp\)AD tại trung điểm của aD
Ta có: BC\(\perp\)AD
BC\(\perp\)AH
AD,AH có điểm chung là A
Do đó: A,H,D thẳng hàng
=>BC\(\perp\)AH tại trung điểm của AD
=>H là trung điểm của AD
Xét tứ giác ABDE có
H là trung điểm chung của AD và BE
=>ABDE là hình bình hành
Hình bình hành ABDE có AD\(\perp\)BE tại H
nên ABDE là hình thoi
b: Gọi O là trung điểm của CE
Xét (O) có
ΔCKE nội tiếp
CE là đường kính
Do đó: ΔCKE vuông tại K
=>CK\(\perp\)KE tại E
=>EK\(\perp\)AC tại K
Ta có: EK\(\perp\)AC
AB\(\perp\)AC
Do đó: EK//AB
mà ED//AB(ABDE là hình thoi)
và EK,ED có điểm chung là E
nên E,D,K thẳng hàng

a)\(đkx\ge1,x\ne-1\)
\(\sqrt{\dfrac{x-1}{x+1}}=2\)
\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)
\(\Leftrightarrow x-1=4x-4\)
\(\Leftrightarrow x=1\)(nhận)
Vậy S=\(\left\{1\right\}\)
c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)
\(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)
\(\Leftrightarrow5x-1+2x=1\)
\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)
Vậy S=\(\left\{\dfrac{2}{7}\right\}\)
c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\left|5x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)






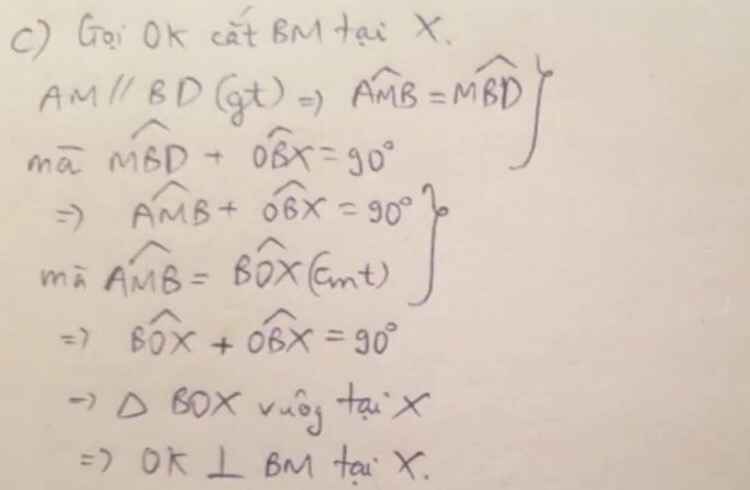
 a, b thôi ạ!
a, b thôi ạ!
a: góc MBO+góc MCO=180 độ
=>MBOC nội tiếp
Xét (O) có
MB,MC là tiếp tuyến
=>MB=MC
mà OB=OC
nên OM là trung trực của BC
=>I là trung điểm của BC