Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=x^2-2x+1=\left(x-1\right)^2\ge0\) ;\(\forall x\in R\)
\(\Rightarrow\) Hàm đồng biến trên R

a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)

Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a), b) và với đường thẳng y = -1 ở câu c).
a) Xét hàm số y = x3 – 3x2 + 5 . Tập xác định : R.
y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0,x = 2.
Bảng biến thiên:
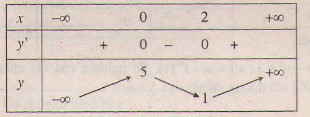
Đồ thị như hình bên.
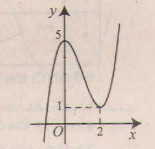
Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
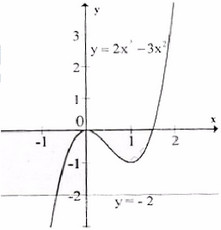
b) Xét hàm số y = -2x3 + 3x2 - 2 . Tập xác định : R.
y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.

Đồ thị như hình bên. Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
c) Xét hàm số y = f(x) = 2x2 - 2x4. Tập xác định : R.
y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên:
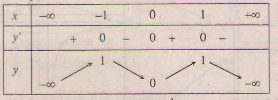
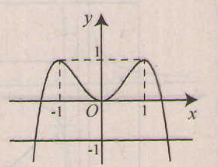
Đồ thị hàm số f(x) và đường thẳng y = -1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.

\(D=\left[0;\pi\right]\)
\(y'=2\cos x-2\sin2x=2\cos x-4\cos x.\sin x=2\cos x\left(1-2\sin x\right)\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}2\cos x=0\\1-2\sin x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\cos x=0\\\sin x=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\left(tm\right)\\x=\dfrac{\pi}{6}\left(tm\right)\\x=\dfrac{5\pi}{6}\left(tm\right)\end{matrix}\right.\)
Bảng biến thiên:
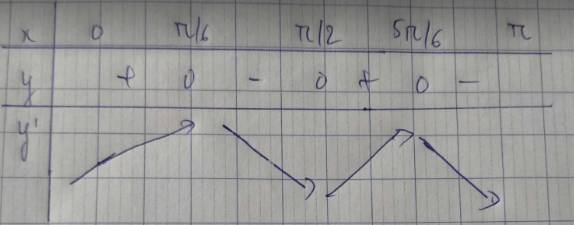
=> Hàm số y động biến trên \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
-> Chọn C

\(log\left(5\left(x^2+1\right)\right)\ge log\left(mx^2+4x+m\right)\)
- BPT đúng \(\forall x\Rightarrow log\left(mx^2+4x+m\right)\) xác định \(\forall x\in R\)
\(\Rightarrow mx^2+4x+m>0\) \(\forall x\in R\)
\(\Rightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=4-m^2< 0\end{matrix}\right.\) \(\Rightarrow m>2\) (1)
- Lại có \(x^2+1\ge1\) \(\forall x\)
\(\Rightarrow5\left(x^2+1\right)\ge mx^2+4x+m\)
\(\Leftrightarrow5\left(x^2+1\right)-4x\ge m\left(x^2+1\right)\)
\(\Leftrightarrow5-\dfrac{4x}{x^2+1}\ge m\)
Đặt \(f\left(x\right)=5-\dfrac{4x}{x^2+1}\Rightarrow f\left(x\right)\ge m\) \(\forall x\Leftrightarrow m\le min\left(f\left(x\right)\right)\)
Ta có \(f\left(x\right)=3+2-\dfrac{4x}{x^2+1}=3+\dfrac{2\left(x-1\right)^2}{x^2+1}\ge3\)
\(\Rightarrow min\left(f\left(x\right)\right)=3\Rightarrow m\le3\) (2)
Kết hợp (1), (2) \(\Rightarrow2< m\le3\Rightarrow m=3\)
Vậy có 1 giá trị nguyên duy nhất của m để BPT đúng với mọi x
Đáp án B

\(y'=-3x^2+6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Hàm đồng biến trên \(\left(0;2\right)\)