
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

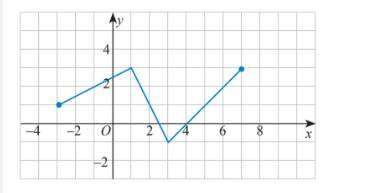
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

a) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( {0; + \infty } \right) \Rightarrow {x_1}{x_2} > 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( { - \infty ;0} \right) \Rightarrow {x_1}{x_2} > 0\)(Cùng dấu âm nên tích cũng âm)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\).

Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)

Hàm số nghịch biến là kiến thức trọng tâm của chương trình toán phổ thông
chắc vậy
học tốt
Hàm số nghịch biến khi a<0
Em mới học lớp 9 thui! Không biết đây có phải đáp án đúng kô