Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi thời gian tổ A; tổ B đã làm lần lượt là: x;y(h)
năng suất của tổ A là 1/20(công việc/h)
năng suất của tổB là: 1/15(công viêc/h)
khối lượng công việc tổ A làm được trong x giờ là: x/20(công việc)
khối lượng công việc tổ B làm được trong y giờ là: y/15(công việc)
vì nếu tổ A làm việc trong x giờ rồi nghỉ và tổ B làm tiếp trong y giờ thì xong công việc nên ta có phương trình: x20+y15=1⇔3x+4y=60(1)x20+y15=1⇔3x+4y=60(1)
vì tổ A làm ít hơn tổ B 3h20'=10/3 h nên ta có phương trình
y-x=10/3(2)
từ (1) và (2) ta có hệ phương trình:
{3x+4y=60y−x=103⇔{y=10x=203{3x+4y=60y−x=103⇔{y=10x=203 (tm)
vậy thời gian tổ A; tổ B đã làm lần lượt là 20/3 h và 10h

Bài 1
a/ Ta có : Góc AOK = góc xAC ( AC // OB )
Góc xAC = góc AEC ( góc tạo bởi t.t và dây cung và góc nt chắn cung AC )
Góc AEC = góc OEK ( 2 góc đối đỉnh )
=> góc AOK = góc OEK
Xét tam giác KOE và tam giác KAO ta có:
Góc OKE = góc OKA ( góc chung )
Góc OEK = góc AOK ( cmt )
=> tam giác KOE đồng dạng tam giác KAO (g-g)
=> \(\frac{KO}{KA}=\frac{KE}{KO}\)=>\(KO^2=KA.KE\)(1)
b/ Xét tam giác BEK và tam giác AKB ta có :
Góc EKB = góc AKB ( góc chung )
Góc EBK = góc BAK ( góc tạo bởi t.t và dây cung và góc nt chắn cung EB )
=> tam giác BEK đồng dạng tam giác ABK (g-g)
=> \(\frac{KE}{KB}=\frac{KB}{KA}\)=>\(KB^2=KE.KA\)(2)
(1) và (2) => \(KO^2=KB^2\)=>\(KO=KB\)=> K là trung điểm OB

à minh ghi thiếu, bài 2 là người ta giao cho tổ A làm trong một thời gian nhất định

Gọi thời gian đội 1 làm một mình là \(x\left(h\right)\left(x>0\right)\)
\(1h\) đội 1 làm được \(\frac{1}{x}\left(V\right)\)
Gọi thời gian đội 2 làm một mình là \(y\left(h\right)\left(y>0\right)\)
\(1h\) đội 2 làm được \(\frac{1}{y}\left(V\right)\)
Ta có: \(\frac{1}{x}+\frac{1}{y}=\frac{1}{4}\)
\(\Leftrightarrow y-x=6\)
\(\Rightarrow y=6+x\)
\(\Rightarrow\frac{1}{x}+\frac{1}{6+x}=\frac{1}{4}\)
\(\Leftrightarrow4\left(6+x\right)+4x=x^2+6x\)
\(\Leftrightarrow24+8x=x^2+6x\)
\(\Leftrightarrow x^2-2x-24=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=6\\x=-4\left(l\right)\end{cases}}\)
Vậy đội 1 làm trong \(6h\); đội 2 làm trong \(12h\)

Gọi thời gian tổ 1 làm một mình xong công việc là x(h); thời gian tổ 1 làm một mình xong công việc là y(h) (ĐK: x, y > 0)
Một giờ tổ 1 làm được: \(\dfrac{1}{x}\) (Công việc)
Một giờ tổ 2 làm được: \(\dfrac{1}{y}\) (Công việc)
Một giờ cả hai tổ làm được: \(\dfrac{1}{12}\) (Công việc)
Vì một giờ cả hai tổ làm được \(\dfrac{1}{12}\) công việc nên ta có pt:
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\) (1)
Tổ 1 làm chung với tổ 2 trong 4 giờ thì phải đi làm việc khác nên tổ 1 làm được: \(\dfrac{4}{x}\) (Công việc)
Tổ 2 làm chung với tổ 1 trong 4 giờ và làm xong công việc còn lại trong 10 giờ nên tổ 2 làm được: \(\dfrac{4}{y}+\dfrac{10}{y}=\dfrac{14}{y}\) (Công việc)
Vì hai tổ làm xong 1 công việc nên ta có pt:
\(\dfrac{4}{x}+\dfrac{14}{y}=1\) (2)
Từ (1) và (2) ta có hpt:
(I) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)
Giải hpt:
(I) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{1}{3}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}-\dfrac{10}{y}=\dfrac{-2}{3}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}y=15\\\dfrac{4}{x}+\dfrac{14}{15}=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}y=15\\\dfrac{4}{x}=\dfrac{1}{15}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\) (TM)
Vậy tổ 1 làm một mình trong 60h thì xong công việc đó
tổ 2 làm một mình trong 15h thì xong công việc đó
Chúc bn học tốt!
Gọi thời gian tổ 1 làm một mình xong công việc là x(h); thời gian tổ 1 làm một mình xong công việc là y(h) (ĐK: x, y > 0)
Một giờ tổ 1 làm được: 1x1x (Công việc)
Một giờ tổ 2 làm được: 1y1y (Công việc)
Một giờ cả hai tổ làm được: 112112 (Công việc)
Vì một giờ cả hai tổ làm được 112112 công việc nên ta có pt:
1x+1y=1121x+1y=112 (1)
Tổ 1 làm chung với tổ 2 trong 4 giờ thì phải đi làm việc khác nên tổ 1 làm được: 4x4x (Công việc)
Tổ 2 làm chung với tổ 1 trong 4 giờ và làm xong công việc còn lại trong 10 giờ nên tổ 2 làm được: 4y+10y=14y4y+10y=14y (Công việc)
Vì hai tổ làm xong 1 công việc nên ta có pt:
4x+14y=14x+14y=1 (2)
Từ (1) và (2) ta có hpt:
(I) ⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩1x+1y=1124x+14

gọi thời gian tổ A; tổ B đã làm lần lượt là: x;y(h)
năng suất của tổ A là 1/20(công việc/h)
năng suất của tổB là: 1/15(công viêc/h)
khối lượng công việc tổ A làm được trong x giờ là: x/20(công việc)
khối lượng công việc tổ B làm được trong y giờ là: y/15(công việc)
vì nếu tổ A làm việc trong x giờ rồi nghỉ và tổ B làm tiếp trong y giờ thì xong công việc nên ta có phương trình: \(\frac{x}{20}+\frac{y}{15}=1\Leftrightarrow3x+4y=60\left(1\right)\)
vì tổ A làm ít hơn tổ B 3h20'=10/3 h nên ta có phương trình
y-x=10/3(2)
từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x+4y=60\\y-x=\frac{10}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=10\\x=\frac{20}{3}\end{matrix}\right.\) (tm)
vậy thời gian tổ A; tổ B đã làm lần lượt là 20/3 h và 10h

Gọi năng suất của tổ 1 là x (x > 0, phần công việc/giờ)
Vì hai tổ sản xuất cùng làm chung công việc thì hoàn thành trong 2 giờ nên năng suất của tổ 2 là: ½ - x (phần công việc/giờ)
Thời gian tổ 1 làm 1 mình xong công việc là: 1/x (giờ)
Thời gian tổ 2 làm 1 mình xong công việc là: 1 1 2 - x (giờ)
Vì khi làm riêng, tổ một hoàn thành sớm hơn tổ hai là 3 giờ nên ta có phương trình:
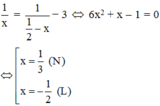
Vậy thời gian tổ 1 hoàn thành công việc một mình là 3 giờ
Đáp án: A

Gọi năng suất của tổ 1 là x (x > 6, phần công việc/giờ)
Vì hai tổ sản xuất cùng làm chung công việc thì hoàn thành trong 6 giờ nên năng suất của tổ 2 là: 1/6 – x (phần công việc/giờ);
Thời gian tổ 1 làm một mình xong công việc là: 1/x (giờ)
Thời gian tổ 2 làm một mình xong công việc là: 1 1 6 - x (giờ)
Vì khi làm riêng tổ một hoàn thành sớm hơn tổ hai là 5 giờ nên ta có phương trình:

Vậy thời gian tổ 1 hoàn thành công việc một mình là 10 giờ
Đáp án: B

Lấy 2 giờ của người thứ nhất để làm chung với người thứ hai thì được \(\frac{1}{3}-\frac{1}{15}=\frac{4}{15}\) (công việc)
2 giờ còn lại của người thứ nhất làm được \(30\%-\frac{4}{15}=\frac{3}{10}-\frac{4}{15}=\frac{1}{30}\)
Thời gian người thứ nhất làm xong công việc là :
2 : \(\frac{1}{30}\) = 60 (giờ)
3 giờ người thứ hai làm được \(\frac{4}{15}-\frac{1}{30}=\frac{7}{30}\)
Thời gian người thứ hai làm xong công việc là :
\(3:\frac{7}{30}=\frac{90}{7}\) (giờ)