Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: BN//AC
OC\(\perp\)AC
Do đó: BN\(\perp\)OC
=>BN\(\perp\)CD
b: Sửa đề: BOCA nội tiếp
Xét tứ giác BOCA có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên BOCA là tứ giác nội tiếp

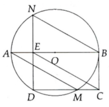
a, HS tự chứng minh
b, Ta chứng minh được tứ giác BCEN là hình bình hành => BC = EN
Do BCDE là hình bình hành
=> BC = ED; DE = EN
=> BA ⊥ EN => BABC
=> BC là tiếp tuyến

b, Vì DF//AB nên \(\widehat{DHC}=\widehat{BAC}\)(đồng vị)
mà \(\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\widehat{DOC}\)(góc nội tiếp và góc ở tâm)
\(\Rightarrow\widehat{DOC}=\widehat{DHC}\)hay tứ giác DOHC nội tiếp
\(\Rightarrow\widehat{DHO}=\widehat{DCO}=90^0\)\(\Rightarrow OH\perp DF\)
câu c tí nữa làm :P
c, Từ a, b => 5 điểm B,O,H,C,D cùng nằm trên đường tròn đường kính OD
Vì tứ giác BHCD nội tiếp \(\Rightarrow ID.IH=IB.IC\)
Vì tứ giác BECF nội tiếp \(\Rightarrow IE.IF=IB.IC\)
\(\Rightarrow ID.IH=IE.IF\)