Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có F = k q 1 q 2 ε r 2 → q 1 q 2 = ε r 2 F k → q 1 q 2 = 1 , 8 9.10 9 = 2.10 10
Do hai điện tích đẩy nhau nên chúng cùng dấu, tức là
q 1 q 2 > 0 → q 1 q 2 = 2.10 − 5 q 1 + q 2 = 3.10 − 5
Áp dụng định lí Viet, ta có q 1 v à q 2 là nghiệm của phương trình bậc 2: q 2 − S q + P = 0
Hay q 2 − 3.10 − 5 q + 2.10 − 5 = 0 → q 1 = 10 − 5 C q 2 = 2.10 − 5 C
hoặc q 1 = 2.10 − 5 C q 2 = 10 − 5 C
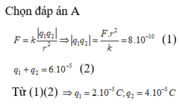
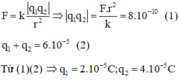
Tóm tắt: q1+q2=7.10-6C (1), r=0,1m
\(F=k\frac {|q_{1}q_2|} {r^2}<=>|q_1q_2|=\frac {Fr^2} {k}=\frac {1} {9000}\)
Vì hai điện tích đẩy nhau nên q1 và q2 cùng dấu <=>q1q2>0 <=> q1q2=\(\frac {1} {9000}\)(2)
(1) (2) => q1, q2 là hai nghiệm phương trình bậc hai Q2-SQ+P=0
(Theo định lý Viète bạn đọc phần áp dụng https://vi.wikipedia.org/wiki/%C4%90%E1%BB%8Bnh_l%C3%BD_Vi%C3%A8te nha cái này cấp 2 có học rồi)
Với S=q1+q2=7.10-6C; P=q1q2=\(\frac {1} {9000}\)
<=>Q2-7.10-6Q+\(\frac {1} {9000} \)=0
Sử dụng máy tính cầm tay ta thấy phương trình vô nghiệm (xuất hiện đơn vị ảo i)
Chắc là bạn cho sai đề rồi nhé mình nghĩ là phương trình có nghiệm nếu F bạn hạ thấp xuống, mình nghĩ bạn cho F=108N là lớn quá không thực tế được đâu mình sẽ sửa lại là F=10N thôi nhé
Làm theo các bước như trên ta có q1+q2=7.10-6C (1)
và \(F=k\frac {|q_{1}q_2|} {r^2}<=>|q_1q_2|=\frac {Fr^2} {k}≈\)1,11.10-11
Chính xác là q1q2=\(\frac {10} {9}\).10-11 (mình bỏ dấu trị tuyệt đối đi vì hai điện tích cùng dấu nhé)
Khi đó q1, q2 là hai nghiệm phương trình Q2-7.10-6Q+\(\frac {10} {9}\).10-11=0
Sử dụng máy tính ta được q1≈±4,57.10-6C; q2≈±2,43.10-6C
Mình sử dụng dấu cộng trừ vì nếu q1, q2<0 thì vẫn thỏa mãn điều kiện bài toán (âm đẩy âm)
Đáp án này là của mình nhé, bạn có thể coi kĩ lại đề, hoặc nếu đề ghi vậy thì nó sai rồi đó. Chủ yếu trong này cần vài phép biến đổi từ biểu thức định luật Coulomb và áp dụng định lý Viète (Vi-ét) đã học ở cấp 2 thôi.