Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian người 1, người 2 làm một mình xong công việc lần lượt là x, y ngày (x, y > 0)
Trong một ngày người 1 và người 2 lần lượt làm được và công việc.
suy ra phương trình:
Người 1 làm trong 3 ngày và người 2 làm trong 7,5 ngày lần lượt được và công việc suy ra phương trình:
Giải hệ được x = 18, y = 9. So sánh với điều kiện và kết luận
người thứ nhất :18 ngày
người thứ hai :9 ngày phải hông ? kiểm tra giùm nghe

Gọi thời gian người 1 làm thì xog cvc là x(ngày)(x>2)
Thời gian người 2 làm thì xog cvc là y (ngày)(y>2)
Trong 1 ngày: người 1 làm đc 1/x(cvc)
người 2 làm:1/y(cvc)cả 2 làm đc 1/2cvc
Theo bài ra ta có hệ pt: {1/x+1/y=1/2
{4/x+1/y=1
giải ra x=6 ngày, y=3 ngày (tm)
Người thứ nhất làm 1 mk trong 6 ngày xog cvc
người thứ 2 làm 1 mk trong 3 ngày xog cvc
Gọi thời gian người thứ nhất làm một mình xong công việc là x ( x>2)
Gọi thời gian người thứ hai làm một mình xong công việc là y ( y>2)
Trong 1 ngày:
-Người thứ 1 làm được : \(\dfrac{1}{x}\) Công việc
-Người thứ 2 làm được: \(\dfrac{1}{y}\) Công việc
-Cả 2 người làm được \(\dfrac{1}{2}\) Công việc
Ta có PT: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\)(1)
-Nếu người nhất làm trong 4 ngày rồi nghỉ, người thứ hai làm tiếp trong một ngày nữa thì xong việc nên ta có PT:
\(\dfrac{4}{x}+\dfrac{1}{y}=1\) (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\\\dfrac{4}{x}+\dfrac{1}{y}=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=6\\y=3\end{matrix}\right.\)
Vậy người thứ nhất làm một mình xong công việc trong 6 ngày
Vậy người thứ hai làm một mình xong công việc trong 3 ngày

Gọi x, y (ngày) lần lượt là thời gian mà người thứ nhất và người thứ hai làm riêng xong công việc. Điều kiện: x > 4, y > 4.
Như vậy, trong 1 ngày người thứ nhất làm được 1/x (công việc), người thứ hai làm được 1/y (công việc).
Trong 1 ngày, cả hai người làm được 1 : 4 = 1/4 (công việc)
Ta có phương trình: 1/x + 1/y = 1/4
Nếu người thứ nhất làm một mình trong 9 ngày rồi người thứ hai đến cùng làm tiếp trong 1 ngày nữa thì xong việc, ta có phương trình:
10/x + 1/y = 1
Ta có hệ phương trình:
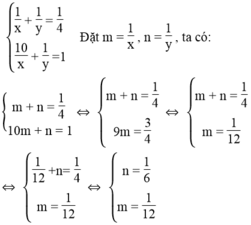
Ta có: 1/x = 1/12 ⇔ x = 12
1/y = 1/6 ⇔ y = 6
Giá trị của x và y thỏa điều kiện bài toán.
Vậy người thứ nhất làm một mình xong công việc trong 12 ngày, người thứ hai làm một mình xong công việc trong 6 ngày.
Sao lại có số 10 vậy bạn , người thứ nhất làm xong 9 ngày mà có số 10 nên mik ko hiểu lắm ??

Gọi thời gian người thứ nhất hoàn thành công việc khi làm một mình là x(giờ)(Điều kiện: x>24)
Thời gian người thứ hai hoàn thành công việc khi làm một mình là:
x-20(ngày)
Trong 1 ngày, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 ngày, người thứ hai làm được: \(\dfrac{1}{x-20}\)(công việc)
Trong 1 ngày, hai người làm được: \(\dfrac{1}{24}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{x-20}=\dfrac{1}{24}\)
\(\Leftrightarrow\dfrac{24\left(x-20\right)}{x\left(x-20\right)}+\dfrac{24x}{24x\left(x-20\right)}=\dfrac{x\left(x-20\right)}{24x\left(x-20\right)}\)
Suy ra: \(x^2-20x=24x-480+24x\)
\(\Leftrightarrow x^2-68x+480=0\)
\(\Delta=\left(-68\right)^2-4\cdot1\cdot480=2704\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{68-52}{2}=8\left(loại\right)\\x_2=\dfrac{68+52}{2}=\dfrac{120}{2}=60\left(nhận\right)\end{matrix}\right.\)
Vậy: Người thứ nhất cần 60 ngày để hoàn thành công việc khi làm một mình
Người thứ hai cần 40 ngày để hoàn thành công việc khi làm một mình
