Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:(P)//(Q)
a vuông góc (P)
=>a vuông góc (Q)
b: Chúng sẽ song song với nhau

Giả sử góc tạo bởi đường thẳng dành cho người khuyết tật và mặt phẳng nằm ngang là α
Vì độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá \(\frac{1}{{12}}\)nên ta có
\(\tan \alpha \le \frac{1}{{12}} \Rightarrow \alpha \le 4,{76^0}\)
Vậy góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá 4,760

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.

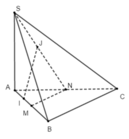
+ Ta có S A B ⊥ A B C S A C ⊥ A B C S A C ∩ S A B = S A ⇒ S A ⊥ A B C
+ Xác định điểm N, mặt phẳng qua SM và song song với BC cắt AC tại N ⇒ N là trung điểm của AC (MN//BC).
+ Xác định được góc giữa hai mặt phẳng (SBC) và (ABC) là S B A ^ = 60 °
⇒ SA = AB.tan 60 ° = 2a 3
AC = A B 2 + B C 2 = 2 a 2
+ Gọi IJ là đoạn vuông góc chung của AB và SN (điểm I thuộc AB và điểm J thuộc SN). Vậy khoảng cách giữa AB và SN là IJ. Ta sẽ biểu thị IJ → qua ba vectơ không cùng phương A B → ; A C → ; A S → .
I J → = I A → + A N → + N J → = m A B → + 1 2 A C → + p N S → = m A B → + 1 2 A C → + p N A → + A S → = m A B → + 1 − p 2 A C → + p A S →
Ta có: I J → ⊥ A B → I J → ⊥ N S → ⇔ I J → . A B → = 0 I J → . N S → = 0
Thay vào ta tính được m = -6/13; p = 1/13
Do đó: I J → = − 6 13 A B → + 6 13 A C → + 1 13 A S → . Suy ra
169 I J 2 = 36 A C 2 + 36 A B 2 + A S 2 − 72 A B → . A C → .
Thay số vào ta tính được IJ = 2 a 39 13 .
Vậy d(AB; SN) = 2 a 39 13 .
Đáp án D

Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)

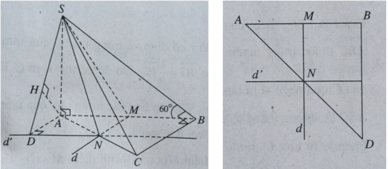
Nhận xét
Gọi (α) là mặt phẳng qua SM và song song với AB.
Ta có BC // (α) và (ABC) là mặt phẳng chứa BC nên (ABC) sẽ cắt (α) theo giao tuyến d đi qua M và song song với BC, d cắt AC tại N.
Ta có (α) chính là mặt phẳng (SMN). Vì M là trung điểm AB nên N là trung điểm AC.
+ Xác định khoảng cách.
Qua N kẻ đường thẳng d’ song song với AB.
Gọi (P) là mặt phẳng đi qua SN và d’.
Ta có: AB // (P).
Khi đó: d(AB, SN) = d(A, (P)).
Dựng AD ⊥ d’, ta có AB // (SDN). Kẻ AH vuông góc với SD, ta có AH ⊥ (SDN) nên:
d(AB, SN) = d(A, (SND)) = AH.
Trong tam giác SAD, ta có 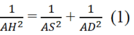
Trong tam giác SAB, ta có S A = A B . tan 60 o = 2 a 3 và AD = MN = BC/2 = a.
Thế vào (1), ta được
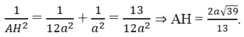

tham khảo:
a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.
b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.
c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.



a) Vì hai mái nhà trong Hình 7.72 là hai hình chữ nhật nên góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà là góc giữa hai đường thẳng OA và OB.
Xét tam giác OAB có
\(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA.OB}} = \frac{{2,{8^2} + {4^2} - 4,{8^2}}}{{2.2,8.4}} = \frac{1}{{28}} \Rightarrow \widehat {AOB} \approx {88^0}\)
b) (OAB) vuông góc với đường nóc nhà, đường nóc nhà song song với mặt phẳng đất nên (OAB) vuông góc với mặt đất phẳng đất.
c) Đường thẳng qua B song song với mặt đất cắt đường thẳng qua A vuông góc với mặt đất tại H
Ta có \(\sin \widehat {ABH} = \frac{{0,5}}{{4,8}} \Rightarrow \widehat {ABH} \approx {6^0};\cos \widehat {OBA} = \frac{{13}}{{16}} \Rightarrow \widehat {OBA} \approx {36^0}\)
Do đó \(\widehat {OBH} = \widehat {ABH} + \widehat {OBA} \approx {42^0}.\)
Vậy góc giữa mái nhà (chứa OB) so với mặt đất khoảng 420