Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)Với y=1 ta có hpt:
\(\int^{2x+3=3+m}_{x+2=m}\Leftrightarrow\int^{2x=m}_{x+2=2x}\Leftrightarrow\int^{2.2=m}_{x=2}\Leftrightarrow\int^{m=4}_{x=2}\)
Vậy nghiệm của hpt là (2;1) khi m=4
b)đợi suy nghĩ
b/=\(\sqrt{x+\left|x-1\right|}-\sqrt{x-\left|x-1\right|}=\sqrt{x}+\left(x-1\right)-\sqrt{x}-\left(x-1\right)\left\{x>1\right\}=\sqrt{x}\left(x-1-x+1\right)\)
\(\int^{\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)}_{2\sqrt{3}x+3\sqrt{5}y=21}\Leftrightarrow\int^{y=\sqrt{5}x-\sqrt{5}\left(\sqrt{3}-1\right)}_{2\sqrt{3}x+3\sqrt{5}\left(\sqrt{5}x-\sqrt{5}\left(\sqrt{3}-1\right)\right)=21}\)
\(\Leftrightarrow\int^{y=\sqrt{5}x-\sqrt{5}\left(\sqrt{3}-1\right)}_{2\sqrt{3}x+15x-15\sqrt{3}+15=21}\Leftrightarrow\int^{y=\sqrt{5}x-\sqrt{5}\left(\sqrt{3}-1\right)}_{\left(2\sqrt{3}+15\right)x=6+15\sqrt{3}}\)
\(\Leftrightarrow\int^{y=\sqrt{5}x-\sqrt{5}\left(\sqrt{3}-1\right)}_{x=\frac{6+15\sqrt{3}}{2\sqrt{3}+15}}\Leftrightarrow\int^{y=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{3}+\sqrt{5}=\sqrt{5}}_{x=\sqrt{3}}\)
Vậy nghiệm của hpt là: \(\int^{x=\sqrt{3}}_{y=\sqrt{5}}\)
ĐK \(x\ne0,y\ne0\)
Hệ\(\Leftrightarrow\hept{\begin{cases}x-y+\frac{x-y}{xy}=0\left(1\right)\\x^3=2y-1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow\left(x-y\right)\left(1+\frac{1}{xy}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=y\\xy=-1\end{cases}}\)
Xét x=y => \(\left(2\right)\Leftrightarrow x^3-2x+1=0\Leftrightarrow\left(x-1\right)\left(x^2+x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\Rightarrow y=1\\x=\frac{-1\pm\sqrt{5}}{2}=y\end{cases}}\)
Xét xy=-1
\(\left(2\right)\Leftrightarrow x^3+\frac{2}{x}+1=0\Leftrightarrow x^4+x+2=0\)(vô nghiệm)
Vậy/////
1)\(\hept{\begin{cases}\sqrt{x}-\sqrt{x-y-1}=1\\y^2+x+2y\sqrt{x}-y^2x=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(\sqrt{x}-1\right)^2=x-y-1\\\left(y+\sqrt{x}\right)^2-y^2x=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-2\sqrt{x}+1=x-y-1\\\left(y+\sqrt{x}-y\sqrt{x}\right)\left(y+\sqrt{x}+y\sqrt{x}\right)=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2\sqrt{x}-y=2\\\left(y+\sqrt{x}-y\sqrt{x}\right)\left(y+\sqrt{x}+y\sqrt{x}\right)=0\end{cases}}\)
Đặt \(\hept{\begin{cases}\sqrt{x}=a\left(\ge0\right)\\y=b\end{cases}}\)
=> hệ phương trình \(\Leftrightarrow\hept{\begin{cases}2a-b=2\\\left(b+a-ab\right)\left(b+a+ab\right)=0\end{cases}}\)
Tham khảo nhé~
Chọn đáp án C
Xét hệ phương trình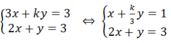
Hai hệ phương trình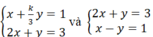
là tương đương khi k/3 = -1 ⇔ k = -3