

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài giải:
Xét bài toán tổng quát:
ABCD là hình thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
AB2 = OA2 +OB2 = ( AC)2 + (
AC)2 + ( BD)2
BD)2
Suy ra AB = 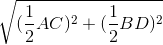
Do đó theo đề bài: AB = 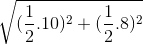
AB = 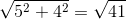
Vậy (B) đúng.
Xét bài toán tổng quát:
ABCD là hình thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
AB2 = OA2 +OB2 = ( AC)2 + (
AC)2 + ( BD)2
BD)2
Suy ra AB = 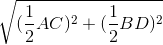
Do đó theo đề bài: AB = 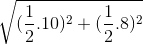
AB = 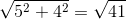
Vậy (B) đúng.

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

O B C D A DB=12cm AC=16cm
Gọi O là gđ 2 đường chéo AC và DB của hình thoi ABCD
Vì DB_|_AC=> OD_|_AC
=>OD là đường cao của tam giác ADC mà AD=DC (t/chất hình thoi)
=> OD là đường trung tuyến của tam giác ADC
=>OA=OC=AC=16/2= 8cm
=> OA=8cm
Vì: AC_|_DB=>OA_|_DB
=> OA là đường cao của tam giác ADB
Mà AD=AB ( theo t/chất hình thoi)
=>OA là đường trung tuyến của tam giác ADB
=>OD=OB=1/2DB=12/2=6cm
=>OD=6 cm
Áp dụng đl pitago vào tam giác vuông AOD có:
OA2+OD2=AD2
=>AD2=82+62
=> AD2=64+36
=> AD2=100
=> AD=5
Vậy độ dài cạnh hình thoi (AD)=5cm

x 6cm 4cm Theo định lý Py - ta - go :
x2 = 42 + 62
⇒ x2 = 16 + 36
⇒ x2 = 52
⇒ x = √52 (cm)
Vậy đáp án (B) là chính xác
Nhắc lại : Đáp án (B)


Ta có hình vẽ :
A D O B F C E
Xét hình thoi ABCD, E và F là chân đường vuông góc kẻ từ đỉnh A đến các cạnh BC, CD. Xét hai trường hợp :
a) Trường hợp EF = \(\frac{1}{2}\) BD
\(\Delta AEC\)= \(\Delta AFC\) (cạnh huyền và góc nhọn) nên CE = CF.
Tam giác cân CEF có CA là đường phân giác của góc C nên CA
Rồi tới bạn làm nốt