
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(11,\\ a,=4\cdot5+14:7=20+2=22\\ b,=3\sqrt{2}-12\sqrt{2}+5\sqrt{2}=-4\sqrt{2}\\ c,=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)}=\dfrac{6}{7}\\ 12,\\ a,P=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ P=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ b,P=\dfrac{1}{2}\Leftrightarrow\sqrt{x}+3=4\Leftrightarrow x=1\left(tm\right)\)
a: \(=4\cdot5+14:7=20+2=22\)
b: \(=3\sqrt{2}-8\sqrt{2}+5\sqrt{2}=0\)

1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)

Câu 6
Thay x=-1 và y=2 vào (d), ta được:
-m+1+2m-3=2
\(\Leftrightarrow m=4\)
Câu 5:
Gọi đths cần tìm là \(y=ax+b\left(a\ne0\right)\)
Vì đt vuông góc với \(y=2x+7\) nên \(2a=-1\Leftrightarrow a=-\dfrac{1}{2}\)
Do đó hệ số góc của đt là \(a=-\dfrac{1}{2}\)

Câu 7:
Thay x=0 và y=9 vào (d), ta được:
-2m-3=9
hay m=-6

câu 1:
đường thẳng (d) song song với đường thẳng y=3x+1 khi a=3
vậy hệ số góc của đường thẳng (d) song song với đường thẳng y=3x+1 là 3
câu 2:
vì góc tạo bởi đường thẳng (d):y=ax+b(a≠0) với trục Ox là 30o nên
\(a=\tan30^o=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
vậy hệ số góc của đường thẳng (d) tạo với trục Ox là\(\dfrac{\sqrt{3}}{3}\)

Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)


Câu 3:
Thay x=-1 và y=0 vào (d), ta được:
-m+2m-1=0
hay m=1










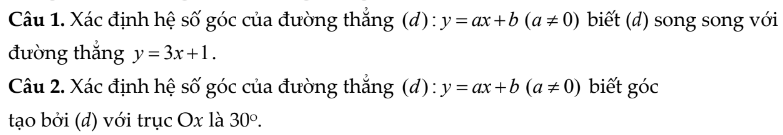


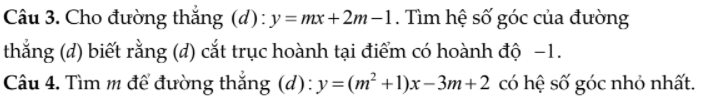 này được
này được
a: \(BC=\sqrt{21^2+72^2}=75\left(cm\right)\)
b: \(AH=\dfrac{21\cdot72}{75}=20.16\left(cm\right)\)
\(BH=\sqrt{21^2-20.16^2}=5.88\left(cm\right)\)
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=75\left(cm\right)\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=5,88\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=20,16\left(cm\right)\end{matrix}\right.\)
c, Vì BD là p/g nên \(\dfrac{AD}{DH}=\dfrac{AB}{BH}=\dfrac{25}{7}\Rightarrow AD=\dfrac{25}{7}DH\)
Mà \(AD+DH=AH\Rightarrow\dfrac{32}{7}DH=20,16\Rightarrow DH=4,41\left(cm\right)\)
\(\Rightarrow AD=15,75\left(cm\right)\)