Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi t1 (giờ) là thời gian người thứ nhất sơn xong bức tường,
t2 (giờ) là thời gian người thứ hai sơn xong bức tường.
(Điều kiện: t1 > 0; t2 > 0)
+ Trong một giờ:
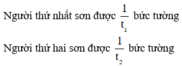
+ Người thứ nhất làm trong 7 giờ và người thứ hai làm trong 4 giờ thì họ sơn được 5/9 bức tường nên ta có: 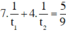
+ Sau đó họ cùng làm việc với nhau trong 4 giờ nữa, nghĩa là người thứ nhất làm trong 7 + 4 = 11 giờ và người thứ hai làm trong 4 + 4 = 8 giờ.
Khi đó họ còn 1/18 bức tường chưa sơn nghĩa là họ đã sơn được 17/18 bức tường.
Ta có phương trình 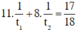
Ta có hệ phương trình 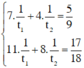
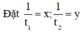 , khi đó hệ phương trình trở thành
, khi đó hệ phương trình trở thành 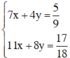
Giải hệ phương trình trên ta được 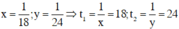
Vậy nếu mỗi người làm riêng thì người thứ nhất sơn xong bức tường trong 18 giờ, người thứ hai sơn xong bức tường trong 24 giờ.

1:
Giải:
Phân số chỉ 1 giờ bác Thành làm được là:
\(1:3=\frac{1}{3}\) ( công việc )
Phân số chỉ 1 giờ bác Mai làm được là:
\(1:4=\frac{1}{4}\) ( công việc)
Phân số chỉ 1 giờ cả hai bác làm được là:
\(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\) ( công việc )
Nếu hai bác cùng làm thì sau số giờ xong công việc là:
\(1:\frac{7}{12}=\frac{12}{7}\) ( giờ )
Vậy nếu cả hai bác cùng làm thì sau \(\frac{12}{7}\) giờ sẽ xong công việc
2:
Giải:
Phân số chỉ 2 giờ người thứ nhất đi được là:
\(2:3=\frac{2}{3}\) ( quãng đường AB )
Phân số chỉ 2 giờ người thứ hai đi được là:
\(2:4=\frac{2}{4}=\frac{1}{2}\) ( quãng đường AB )
Phân số chỉ 5 km là:
\(\frac{2}{3}-\frac{1}{2}=\frac{1}{6}\) ( quãng đường AB )
Quãng đường AB dài là:
\(5:\frac{1}{6}=30\) ( km )
Vậy quãng đường AB dài 30km

Giống bài hpt lớp 8 :
Gọi thời gian người 1 quét sân một mình là a (a>2).
=> Thời gian ngưởi 2 quét sân một mình là a-2.
Trong một giờ người 1 quét được \(\dfrac{1}{a}\)(sân), người 2 quét được \(\dfrac{1}{a-2}\) (sân).
Tổng thời gian nếu hai người quét chung là \(\dfrac{4}{3}\left(h\right)\) nên trong một giờ thì 2 người sẽ làm đc \(\dfrac{3}{4}\) sân.
Lập phương trình : \(\dfrac{1}{x}+\dfrac{1}{x-2}=\dfrac{3}{4}\Leftrightarrow\dfrac{2x-2}{x\left(x-2\right)}=\dfrac{3}{4}\Leftrightarrow3x^2-14x+8=0\)
Phân tích \(3x^2-14x+8\) được hai nghiệm \(\left[{}\begin{matrix}x=4\left(TMĐK\right)\\x=\dfrac{2}{3}\left(KTMĐK\right)\end{matrix}\right.\)
Vậy người 1 quét sân một mình hết 4h, người hai quét sân một mình hết \(4-2=2\left(h\right)\).

– Gọi x (giờ) là thời gian người thứ nhất quét sân một mình (x > 2).
– Khi đó, x – 2 (giờ) là thời gian người thứ hai quét sân một mình.
– Trong 1 giờ:
Người thứ nhất quét được 1/x (sân)
Người thứ hai quét được 1/(x – 2) (sân)
Cả hai người quét được 1/x + 1/(x – 2) (sân).
– Lại theo đề bài: Cả hai người cùng quét sân hết 1 giờ 20 phút = 4/3 giờ nên trong một giờ, cả hai người quét được 3/4 sân.
Vậy ta có phương trình:
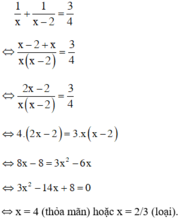
Vậy nếu quét một mình thì người thứ nhất quét hết 4 giờ, người thứ hai hết 2 giờ.

diện tích xung quanh căn nhà là:
(12+4)x2x3,5=112(m2)
diện tích quét sơn (không tính cửa sổ) là:
112-10,2=101,8(m2)
diện tích toàn bộ cần quét sơn là:
101,8+(3,5+2,5)x2x3,5=143,8(m2)
số tiền cần trả là:
143,8x20000=2876000(đồng)
đáp số: 2876000 đồng

Tuần thứ 2 làm được:
2/5*2/3=4/15(đoạn đường)
Phân số tương ứng với 450m là:
1-2/5-4/15=1/3(đoạn đường)
Đoạn đường dài:
450:1/3=1350(m)
ĐS:1350m(câu b)
Tuần đầu làm được:
1350*2/5=540(m)
Tuần thứ hai làm được:
1350-450-540=360(m)
ĐS:...(câu b)

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}} \right)\).
+ Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất nên \(0 \le x \le 200\)
và 240 chiếc mũ kiểu thứ hai nên ta có \(0 \le y \le 240\)
+ Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc
=> Thời gian làm \(1\) chiếc mũ kiểu thứ hai là 1/60 (giờ)
=> Thời gian làm \(y\) chiếc kiểu hai là \(\frac{y}{{60}}\left( h \right)\)
+ Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai
=> thời gian làm 1 chiếc mũ kiểu thứ nhất là 2.1/60 = 1/30 (giờ)
=> Thời gian làm \(x\) chiếc kiểu thứ nhất là \(\frac{x}{{30}}\left( h \right)\)
+ Tổng thời gian làm một ngày không quá 8h nên ta có:
\(\frac{x}{{30}} + \frac{y}{{60}} \le 8\)
Bước 2: Lập hệ bất phương trình.
\(\left\{ \begin{array}{l}
0 \le x \le 200\\
0 \le y \le 240\\
\frac{x}{{30}} + \frac{y}{{60}} \le 8
\end{array} \right.\)
Bước 3: Biểu diễn miền nghiệm.
Miền biểu diễn miền nghiệm là phần không bị gạch, đa giác OABCD với O(0;0), A(0; 240), B(120; 240), C(200; 80), D(200; 0).
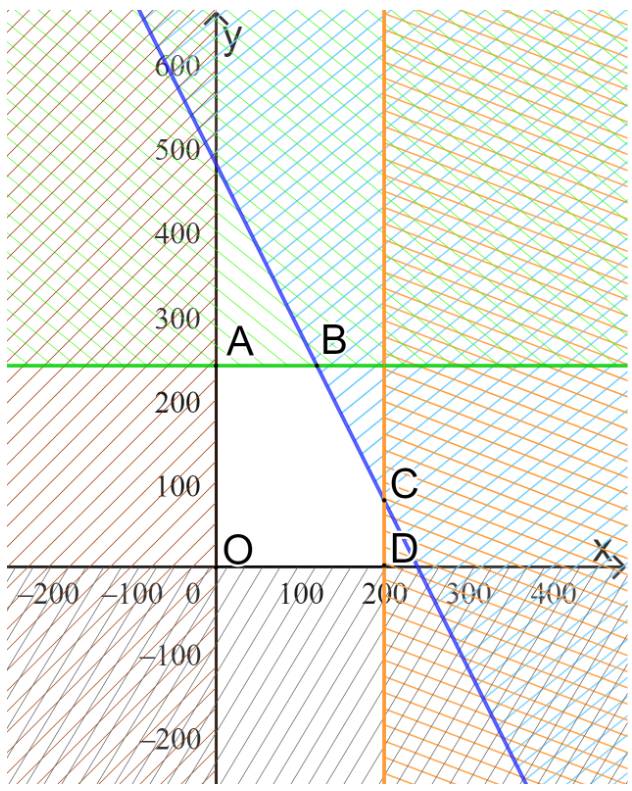
Bước 4: Tìm \(x\) và \(y\) để tiền lãi cao nhất.
Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm \(\left( {x;y} \right)\) là một trong các đỉnh của đa giác OABCD.
\(T = 24x + 15y\)
\(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)
\(T\left( {120;240} \right) = 24.120+15.240 = 6480\) (nghìn đồng)
\(T\left( {200;80} \right) = 24.200+15.80 = 6000\) (nghìn đồng)
\(T\left( {200;0} \right) = 24.200 = 4800\)(nghìn đồng)
Vậy để tiền lãi thu được nhiều nhất, mỗi ngày xưởng cần sản xuất số mũ kiểu 1 là 120 và mũ kiểu 2 là 240 cái.
Gọi x (giờ), y(giờ) là thời gian để công nhân thứ nhất, thứ hai làm riêng để sơn xong bức tường.
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{7}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{4}{y}=1-\dfrac{5}{9}-\dfrac{1}{18}=\dfrac{7}{18}\end{matrix}\right.\)
Giải hệ phương trình trên ta được: \(\dfrac{1}{x}=\dfrac{1}{18};\dfrac{1}{y}=\dfrac{1}{24}\)
Suy ra x = 18, y = 24.
Vậy mỗi người làm riêng, theo thứ tự, thời gian sơn xong bức tường là 18 giờ và 24 giờ.