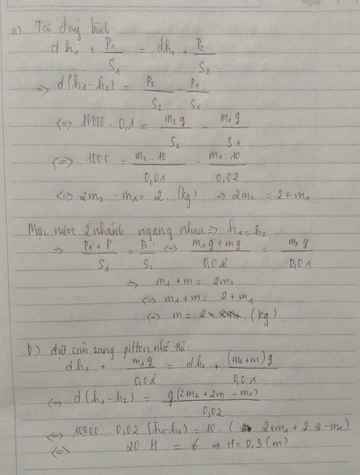Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi đặt cân: \(m=1kg\) lên pittông \(S_1\).
Có: \(pA=pB\Rightarrow\frac{10\left(m_1+m\right)}{S_1}=\frac{10m_2}{S_2}+10Dh_1\)
\(\Rightarrow\frac{m_1+m}{1,5S_2}=\frac{m_2}{S_2}+Dh_1\Rightarrow\frac{m_1+1}{1,5S_2}=\frac{m_2}{S_2}+200\)
\(\Rightarrow\frac{m_1+1}{1,5S_2}-\frac{m_2}{S_2}=200\Rightarrow\frac{m_1+1-1,5m_2}{1,5S_2}=200\)
\(\Rightarrow\frac{2m_2+1-1,5m_2}{S_2}=300\Rightarrow S_2=\frac{1+0,5m_2}{300}\) (*)
* Khi đặt m = 1kg lên pittông S2
\(\Rightarrow PM=PN\Rightarrow\frac{10m_1}{S_1}+10Dh_2=\frac{10\left(m_2+m\right)}{S_2}\)
\(\Leftrightarrow S_2=\frac{1,5-0,5m_2}{75}\) (**)
Thay số vào (*) và (**) tính được: \(m_2=2kg\Rightarrow m_1=4kg\)
Thay m2 vào tính S2 \(=\frac{1}{150}m^2\)
Lập hệ phương trình ra (tự lập) tính được \(x=10cm\)

a. -Áp suất ở mặt dưới pittông nhỏ là :
\(\frac{10m_2}{S_2}=\frac{10m_1}{S_1}+10Dh\Leftrightarrow\frac{m_2}{S_2}=\frac{m_1}{S_1}+Dh\) (*)
- Khi đặt quả cân m lên pittông lớn mực nước ở hai bên ngang nhau nên:
\(\frac{10m_2}{S_2}=\frac{10\left(m_1+m\right)}{S_1}\Leftrightarrow\frac{m_2}{S_2}=\frac{m_1+m}{S_1}\) (**)
Từ (*) (**) có: \(\frac{m_1+m}{S_1}=\frac{m_1}{S_1}+10DH\Leftrightarrow\frac{m_1}{S_1}=D.h\Rightarrow m=2kg\)
b. Khi chuyển quả cân sang pittông nhỏ thì ta có :
\(\frac{10\left(m_2+m\right)}{S_2}=\frac{10m_1}{S_1}+10DH\)
\(\Leftrightarrow\frac{m_2+m}{S2}=\frac{m_1}{S_1}+Dh\)
\(\Rightarrow\frac{m_2+m}{S_2}=\frac{m_1}{S_1}+Dh\) (***)
Kết hợp (*) (**) (***) => H = 30 cm

a)Áp suất ở dưới pittong nhỏ là: \(\dfrac{10m_2}{S_2}=\dfrac{10m_1}{S_1}+10D\cdot h\)
\(\Rightarrow\dfrac{10m_2}{25\cdot10^{-4}}=\dfrac{10\cdot1}{50\cdot10^{-4}}+10\cdot1000\cdot0,1\Rightarrow m_2=0,75kg=750g\)
b)Khi đặt lên pittong bên trái một lượng \(m=300g=0,3kg\) thì nó di chuyển xuống dưới một đoạn:
\(\dfrac{10\left(m_2+m\right)}{S_2}=\dfrac{10m_1}{S_1}+10D\cdot\Delta h\)
\(\Rightarrow\dfrac{10\cdot\left(0,75+0,3\right)}{25\cdot10^{-4}}=\dfrac{10\cdot1}{50\cdot10^{-4}}+10\cdot1000\cdot\Delta h\)
\(\Rightarrow\Delta h=0,22m=22cm\)